ciągłośc funkcji Jolanta:

	x2−9
Prosze o pomoc.zbadaj ciągłośc funkcji f(x)=		dlax∊R−{−1,1}
	1−x2

1 dla x∊{−1,1}

Aruseq: Funkcja f jest ciągła w punkcie x₀, jeśli istnieje lim_x−>x0 f(x), oraz zachodzi: lim_x−>x0 f(x) = f(x₀) W tym przypadku:

	−8
limx−>(−1) f(x) = [		] = −∞
	0

	−8
limx−>(1) f(x) = [		] = −∞
	0

granice w punktach {−1, 1} nie istnieją, gdyż w tych punktach granica funkcji jest niewłaściwa

ABC: A mi się wydaje że granice w punktach −1 ,1 nie istnieją bo granice lewostronne i prawostronne są różne ale co ja tam wiem

chichi: @Aruseq liczymy granice jednostronne... poza tym jak Tobie tam wyszły −∞ to ja nie wiem

chichi: lim_x→−1⁻f(x) = +∞ ∧ lim_x→−1⁺f(x) = −∞ lim_x→1⁻f(x) = −∞ ∧ lim_x→1⁺f(x) = +∞

Jolanta: Dziękuję i proszę o cierpliwość bo próbuję sobie co nieco przypomnieć Dlaczego przy x→−1⁻jest + a nie −∞

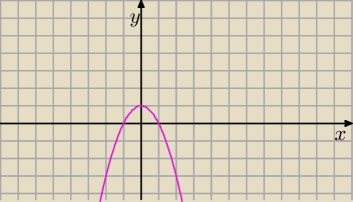
chichi: gdybyś narysowała wykres y = 1 − x² zobaczyłabyś, że jak x dąży do −1 z lewej strony, to wartosci funkcji zbliżają się do 0, ale pod osią OX, czyli blisko −1 są ujemne wartości,

	−8
zatem mamy [		] = +∞
	0−

chichi:

Jolanta: Dziękuję