czworokat abcd i os symetri magnolia: punkty A (30,32) i b (0,8) sa sasiednimi wierzcholkami czworokarta abcd wpisanego w okrag. prosta x − y + 2 = 0 jest jedyna osia syemtri tego czworokata i zawiera przekatna AC. Oblicz wspolrzedne wierzcholkow c i d

Aruseq: Wyznacz symetralną boku AB. Punkt przecięcia tej symetralnej z prostą x−y+2=0 będzie środkiem okręgu opisanego na tym czworokącie. Punkt C znajdziesz w ten sposób, że środek okręgu jest środkiem odcinka AC. Natomiast punkt D będzie leżał na prostej prostopadłej do AC przechodzącej przez B. Mając to informację masz już pare sposobów na wyznaczenie D.

magnolia: nie rozumie skad wiesz ze tak mozna wyznaczyc C bo d mam wyznaczone z liczenia odleglosci ze wzoru ale c nie wiem jak

Aruseq: Na osi symetrii zawarta musi być średnica tego okręgu, czyli AC jest tą średnicą

magnolia: a jesli wyznaczylam D (6,2) a BC to 3√2 i CD powinno miec taka sama dlugosc to czemu mi nie wychodzi jak chce policzyc z tego C? Podstawiajac ze wzorow na dlugosc majac obie dlugosci i wynik?

Aruseq: Pokaż te obliczenia

magnolia: https://ibb.co/SN9Qfjq

magnolia: i teraz 3√2 = √(6−x)² + (2−x−2)² (ten pierwiastek jest nad caloscia i z tego wychodzi x =3 i jest zle

Aruseq: Tyle, że 3√2 to odległość od prostej y=x+2, a nie punktami B i C

magnolia: to co teraz

Aruseq: Przeczytaj ponownie moją pierwszą wiadomość. To chyba najłatwiejszy sposób. Jeśli nie to możesz teraz wyznaczyć równanie okręgu i punkt C będzie jednym z punktów przecięcia tego okręgu z prostą y=x+2

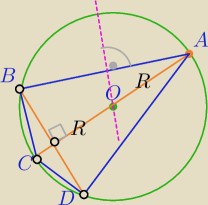
Mila: A =(30,32) i B= (0,8) 1) Prosta AB:

	4
y=		x+8
	5

2) Symetralna: AB

	5		155
y=−		x+
	4		4

3) Oś symetrii czworokąta: y=x+2 zawiera prostą AC Punkt D jest symetryczny do punktu B względem prostej AC D=(6,2) to już wyznaczyłaś − środek okręgu opisanego na czworokącie leży na przecięciu symetralnych jego boków

	5		155
x+2=−		x+
	4		4

	49		55
O=(		,		)
	3		3

O−środek AC

49		xc+30		55		yc+32
	=		i		=
3		2		3		2

98		110
	=xc+30 i		=yc+32
3		3

	8		14
xc=		, yc=
	3		3

	8		14
C=(		,		)
	3		3

D=(6,2) Napisz magnolio , czy taka jest odpowiedź. Mam nadzieję, że Aruseq nie obrazi się za włączenie się do rozwiązywania.

Aruseq: Skądże, warto pokazywać, że każde zadanie ma parę możliwych rozwiązań

Aruseq: Chociaż to chyba ten sam sposób co mój

Mila: Tak, to chyba najłatwiejsze podejście. Równanie okręgu jest kłopotliwe rachunkowo.

magnolia: tak wynik dobry