Aruseq: Okrąg k: (x−2)
2+(y−3)
2=25 K
1=(2,3)
Okrąg k': (x+2)
2+(y+3)
2=25 K
2=(−2, −3)
Tworzymy układ równań, rozwijając wzory skróconego mnożenia:
| ⎧ | x2−4x+4+y2−6y+9=25 | |
| ⎩ | x2+4x+4+y2+6y+9=25 |
|
Równania te wystarczy odjąć od siebie stronami, dostaniemy wtedy zależność:
−8x−12y=0
12y=−8x
y=(−2/3)x − zatem oba te miejsca zerowe leżą na takiej prostej. Podstawiając tego y do jednego
z równań z układu wyliczymy x, mając x możemy obliczyć y. Dostajemy zatem:
Pole tej figury składa się z pól dwóch identycznych trójkątów. Jeden z nich to trójkąt
P
1P
2K
1, a drugi to P
1P
2K
2. Ich podstawy to odcinki P
1P
2 (których długość policzysz z
odległości między punktami), a wysokość, to odległość punku K
1 lub K
2 od prostej, na której
leżą P
1 i P
2, czyli prostej y=(−2/3)y

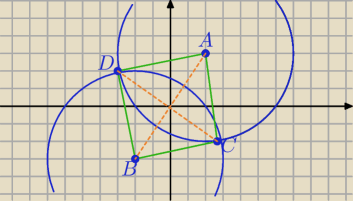 (x−2)2+(y−3)2=25, A=(2,3)
(x+2)2+(y+3)2=25 , B=(−2,−3)
D=(−6√3/13,4√3/13)
C=(6√3/13,−4√3/13)
AB→=[−4,−6],DC→=[12√3/13,−8√3/13]
AB→ o DC→=0 − wektory prostopadłe
(x−2)2+(y−3)2=25, A=(2,3)
(x+2)2+(y+3)2=25 , B=(−2,−3)
D=(−6√3/13,4√3/13)
C=(6√3/13,−4√3/13)
AB→=[−4,−6],DC→=[12√3/13,−8√3/13]
AB→ o DC→=0 − wektory prostopadłe