dowod
adam : Udowodnić
F:R−−>R oraz Limx−>∞ f(x)=∞, Limx−>∞f(x)= −∞
to istnieje c nalezacego do R takie że f(c)=0
17 lis 18:49
chichi:
popraw i uzupełnij polecenie, bo w takiej postaci nie jest to oczywiście zawsze prawdziwe
17 lis 18:52
chichi:
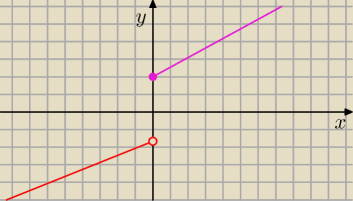
lim
x→−∞f(x) = −
∞ ∧ lim
x→+∞f(x) = +
∞, ale ¬∃c∊R ( f(c) = 0 )
17 lis 18:55