Monotonicznosc ciagu Jupiter: Mam pytanie dotyczące monotoniczności ciągu. Załóżmy, że badam znak różnicy wyrazów i wychodzi mi : −2n+3 To jaki to ciąg? W większości książek jest zapis, że gdy dla każdego n naturalnego w innych jest, że dla n∊N+ a jeszcze w innych, że poza wyrazem pierwszym jest ujemny bądź dodatn. Jest w końcu monotoniczny czy nie?

Aruseq: Jeśli badasz różnicę a_n+1−a_n, to znak różnicy badamy dla każdego n naturalnego dodatniego. Wyrażenie −2n+3 jest dodatnie dla każdego takiego n, więc ciąg ten jest rosnący

chichi: "Wyrażenie −2n+3 jest dodatnie dla każdego takiego n, więc ciąg ten jest rosnący" Chryste Panie...

chichi: @Jupiter mogę zobaczyć wzór ciągu?

Aruseq: Jezu, racja hahahah. Dostałem chwilowego zaćmienia. Zobacz, że dla n=1 różnica jest dodatnia, dla każdego innego n − ujemna. Nie możemy zatem stwierdzić monotoniczności tego ciągu.

Aruseq: W sensie, nie jest on monotoniczny

ABC: jest malejący od pewnego miejsca , można też powiedzieć malejący prawie wszędzie ( za wyjątkiem skończonej liczby początkowych wyrazów)

Jupiter: Dla n=1 jest 1 dla n=2 jest −1 dla n=3 jest −3 dla n=4 jest −5. Itd Tak wiec jest malejący ale pierwsza wartość jest dodatnia, czy to ma znaczenie? Badam znak różnicy i wychodzi: −2m+3 albo z innej −3+5. Czy w tej sytuacji mogę napisac, że różnica jest ujemna dla każdego n naturalnego? Czy może jednak ciąg nie jest monotoniczny ? Niektóre definicje ciągu malejącego mają zapis, że jeśli różnica a_n+1−a_n<0 to jest to ciąg malejący dla każdego n naturalnego oprócz wyrazu pierwszego− wiec jak wniosek powinien być?

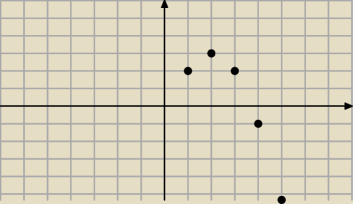
Maciess: Nie jest malejący. Zeby był malejący to wartość wyrażenia −2n+3 powinna być ujemna zawsze tzn. dla każdej liczby natrualnej. Twoj ciąg może wyglądac jak na wykresiku powyzej. Na samym poczatku wartość się zwiększyła, a później maleje. "Czy w tej sytuacji mogę napisac, że różnica jest ujemna dla każdego n naturalnego?" Nie, przecież sam wskazałes n (n=1) dla ktorego to zdanie jest fałszywe "Niektóre definicje ciągu malejącego mają zapis, że jeśli różnica an+1−an<0 to jest to ciąg malejący dla każdego n naturalnego oprócz wyrazu pierwszego− wiec jak wniosek powinien być?" Mozesz podać skąd taka definicja? Generalnie odpowiedź na pytanie czy ciąg jest monotoniczny to: Nie jest. Jeśli to do czegoś potrzebne, można powiedzieć ze ciag jest malejacy od któregoś tam wyrazu.

Jupiter: To było tylko zwykle badanie monotoniczności ciągu. Co do ostatecznego wniosku, wprowadziła Mnie w błąd ta definicja zawierająca zapis o pominięciu pierwszego wyrazu. Wieczorem odnajdę ten zapis i podeśle gdzie został znaleziony. Dziękuję za pomoc. Ostatecznie decyduję, że ciąg nie jest monotoniczny. 😎😀

no już nic nie wiem: no nie do końca Ciąg (an) nazywamy ciągiem malejącym wtedy, gdy dla każdej liczby naturalnej dodatniej n prawdziwa jest nierówność an+1<an. Badamy znak różnicy drugiego i pierwszego wyrazu ale Ciąg 1, 0, −1, −2, −3 też jest ciągiem malejącym chociaż pierwszy wyraz jest dodatni albo np. weźmy rosnący a_n= n²−4n a_n+1−a_n= [(n+1)² – 4(n+1)]− (n² – 4n)= n²+2n+1−4n−4 – n²+4n= 2n−3 i tutaj nie dla każdego n różnica a_n+1−a_n>0 bo np. dla n=1 a₁=−1 pozostałe wyrazy to a₂=1, a₃=3, a₄=5 itd a jednak jest to ciąg rosnący

no już nic nie wiem: @Jupiter moim zdaniem ten twój ciąg jest malejący, bo tak naprawdę w definicji nie chodzi o badanie znaku różnicy a_n+1−a_n<0 i ustalaniu czy to na pewno jest zawsze mniejsze od zera tylko o sprawdzenie czy a_n+1< a_n czyli czy następny wyraz jest mniejszy od poprzedniego