zadanie trgynomietria szlachetny kamien: 3sin²x − 4cos²x sin²x >> 0 w przedziale od minus pi do pi

. : I w czym problem?

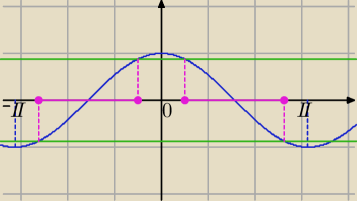
Mila: x∊<−π,π> i 3sin²x − 4cos²x sin²x ≥ 0⇔ sin²x*(3−4cos²x)≥0 sin²x≥0 dla x∊R i

	√3
3−4cos2x≥0⇔|cos(x)|≤		⇔
	2

Daj sam odpowiedź:

szlachetny kamien: ale skąd ta pewność że można podzielić przez takie wyrażenie

Mila: A gdzie tu widzisz dzielenie? sin²x≥0 dla każdego x∊R zatem nie wpływa na zmianę znaku całej nierówności. Dlatego wystarczy rozwiązać nierówność: 3−4cos²x≥0

Mila: I jak to dokończyłeś? Jeszcze jedna podpowiedź : Do rozwiązania nierówności: 3−4cos2x≥0 dołącz rozwiązania równania sin²x=0 z podanego przedziału.