Wektory St : W równolegloscianie o podstawach ABCD i A' B'C' D' równolegle sq krawedzie AA', BB', CC' oraz DD' Jezeli AB = (1,3, −4), AD = [3,1, 0] oraz AA' = (−1,5, 1], toD’C=? AD’=? A’C= CA= Czy mógłby mi ktoś pomoc jak to obliczyć

wredulus_pospolitus: coś chyba nie tak zapisane jest Popraw zapis

St : Tam są wektory powinna być strzałka, ale nie umiem tak zapisać

St : I wszędzie kwadratowy nawias

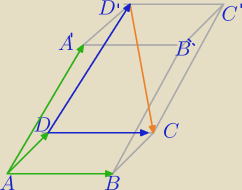
Mila: podpowiedź: AB = [1,3, −4], AD = [3,1, 0] oraz AA' = [−1,5, 1] DD'^→= AA'^→⇒D'C^→=[1,−5,−1]+[1,3,−4]=[2,−2,−6] AD'^→=AD^→+DD'^→= licz

St : AD’=[4,−4,−1]

St : Nie wiem jak to liczyć

St : AD’=[2,6,1]?

St : A’C=[−4,−4,4] CA[4,4,−4] Czy mógłby powiedzieć ktoś xzy to tak?

Mila: Z punktu A do D' możesz przejść po przekątnej albo "po wektorze " AD =[3,1, 0] i wektorze DD'=AA'=[−1,5, 1] 1) AD'→=AD→+DD'→= [3,1, 0] +[−1,5, 1]=[2,6,1] 2) A'C^→: Z punktu A' do punktu C możesz przejść np. po wektorze A'C' i wektorze C'C ( przeciwnym do AA') Liczymy: ( pomijam strzałki) A'C'=A'B'+B'C'=[1,3, −4]+[3,1, 0]=[4,4,−4] A'C=[4,4,−4]+[1,−5,−1=[5,−1,−5] 3) CA : CA=CB+BA=[−3,−1,0]+[−1,−3,4]=[−4,−4,4]

Mila: Ostatni punkt − wsp. CA − można skorzystać z obliczonych wsp. A'C' w pkt. (2)

St : Dziękuje