bijekcja Zum: f: R→R

	1
czy funkcja		jest bijekcją?
	x−1

czy mogę powiedzieć, że nie jest, bo 1 nie należy do dziedziny?

janek191: Tak.

janek191:

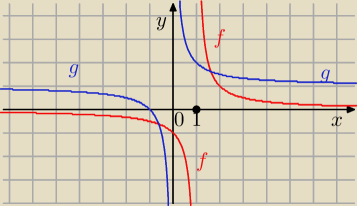
	1
g (x) =		+ 1 − funkcja odwrotna do
	x

chichi: a czy tak zdefiniowana funkcja: f: R\{1} → R\{0}

	1
f(x) =
	x − 1

jest bijekcją?

Zum: hm, tak

chichi: uzasadnij.

Zum: bo jest iniekcją i suriekcją (wiem jak dowieść) miałem tylko wątpliwość czy jak mam f: R→R i istniej jakaś liczba, która jest liczbą rzeczywistą, ale nie należy do dziedziny, to czy od razu na tej podstawie możemy powiedzieć, że funkcja ni jest bijekcją generalnie nie wiem czy dobrze interpretuje zapis f: R→R

I'm back: Dla f: R−> R Funkcja ta jest źle zdefiniowana, ponieważ nie przyjmuje wartości dla x=1 Natomiast nie ma to nic do bijekcji. Nie jest ona bijekcja bo nie jest suriekcja (dla żadnego x funkcja nie przyjmuje wartości 0)

chichi: jeżeli funkcja przyporządkowuje elementom zbioru X elementy zbioru Y, to zapisujemy to tak: f: X → Y, wówczas zbiór X nazywam dziedziną, a zbiór Y − przeciwdziedziną, funkcji (nie mylić ze zbiorem wartości funkcji!), zatem odpowiadając na Twoje pytanie, trudno żeby źle określona w ogóle funkcja była bijekcją

chichi: "Natomiast nie ma to nic do bijekcji." − ojj no ma i to dużo, bijekcja to funkcja wzajemnie jednoznaczna. Funkcja odwzorowuje każdy punkt z dziedziny, w naszym wypadku nie, więc nie ma mowy tu o żadnej funkcji, bo nie jest spełniona definicja

Zum: "f: X → Y, wówczas zbiór X nazywam dziedziną, a zbiór Y − przeciwdziedziną" dzięki, to zdanie mi wiele wyjaśniło

chichi: na zdrowie