proszę o rozwiazanie anna: wyznacz zbiór wartości a) f(x) = log_0,5 ( x² −5x +6) − log_0,5 (x−3) b) f(x) = log_1/3 ( x² −3x +10)

Mila: x²−5x+6>0 i x−3>0⇔x>3

	(x−2)*(x−3)
f(x)=log1/2		=log1/2(x−2)
	x−3

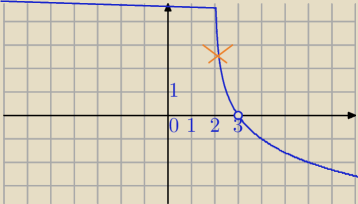
f(x)=log_1/2(x−2) funkcja malejąca f(3)=log_1/2(3−2)=0 f(x)<0 dla x>3

Mila: b) x²−3x+10 >0 dla x∊R f(x)= log_1/3 ( x² −3x +10) Zbiór wartości g(x)=x²−3x+10

	3		31
p=		, q=
	2		4

	31
Zwg=<		,∞)
	4

	31		3
f(3/2)=ln1/3 (		)=ln1/3(31)−2ln1/3(2)− największa wartość f(x) dla x=
	4		2

f(x)<ln_1/3(31)−2ln_1/3(2)≈−1,9

anna: czy w punkcie a) mogę zapisać że zbiór wartości Zw_f = ( − ∞ ; 0 > a w b) Zw_f = (− ∞ ³¹₄ >

anna: f(x)<ln_1/3(31)−2ln_1/3(2)≈−1,9 jak to jest obliczone i jeszcze pytanie czy ln to log

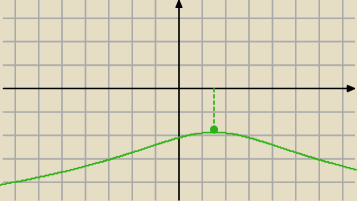
Mila: a) f(x)<0 dla x>3⇔ Zw_f=(−∞,0) w punkcie x=3 masz kółko otwarte, x=3 nie należy do dziedziny b) Zw_f=(−∞,( ln_1/3(31)−2ln_1/3(2) )> masz powyżej wykres tej funkcji (zielony)

anna: dziękuję bardzo