planimetria Kamila: Dany jest trójkąt prostokątny ABC, w którym AC =8 i BC=6. Kat prosty znajduje sić przy wierzchołku C. Odcinek CP jest wysokością trójkąta ABC, a odcinek PQ jest wysokością trójkąta CPA. Oblicz stosunek pola trójkąta APQ do pola trójkata ABC. Pole trójkata ABC jest równe 6*8*1/2=24. Przeciwprostokatna AB wynosi 10 (z te. pitagorasa) z tego wiemy że PC jest równe 24=1/2 AB* PC, czyli PC =4,8 i nie wiem co dalej...

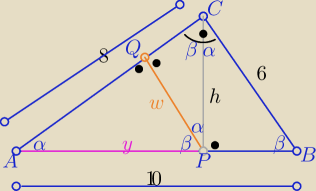
K8: Trójkaty ABC, APQ , APC są podobne z cechy (kkk) to

	8		y
		=		⇒ y=6,4
	10		8

	6,4
to skala podobieństwa Δ APQ do ΔABC : k=		= 0,64
	10

zatem

	P(APQ)
		= k2= ...........
	P(ABC)

i po ptokach

K8: 2 sposób h= 4,8 z tw. Pitagorasa w ΔAPC: y=√8²−4,8² ⇒ y=6,4 skala podobieństwa ΔAPQ i ΔABC

	6,4
k=		= 0,64
	10

P(APQ)
	=k2=..........
P(ABC)

Kamila: Dziekuję pięknie