trójkaty Kamila: W trójkacie prostokatnym dwusieczna jednego z kątów ostrych podzieliła przeciwległą przyprostokątną na odcinki 2i 2,5. Długość przeciwprostokątnej jest równa? Wiem z twierdzenia o dwusiecznej, że stosunek długości przyprostokątnej przyległej do podzielonego kąta i przeciwprostokątnej będzie równy stosunkowi na jaki została podzielona na przeciwległa przyprostokatna, ale dalej co? Jak mam b/c=2,5/2 i 4,5²+ b²=c² ( z tw. Pitagorasa) to wychodzi mi zły wynik

Pitbull puppies forever!: bo muisz uklad b/a =5/4 a drugie równanie b²+a²=(4,5)² przecież c=2+2,5

Pitbull puppies forever!: a nie sorry tak by bylo gdyby dwusieczna kąta prostego

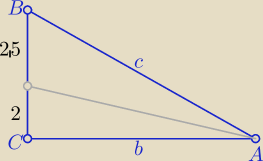
K8: Z tw. o dwusiecznej :

b		2		b		4		4
	=		⇒		=		⇒b=		c
c		2,5		c		5		5

z tw. Pitagorasa

	16
c2= 4,52+		c2
	25

	9		81
		c2=		.c>0
	25		4

c= 7,5 ======

Kamila: Dziękuję bardzo za rozwiązanie, już wiem co było źle. Oznaczyłam b do c jako 2,5 do 2 i wtedy jest bez sensu, bo przeciwprostokatna nie może być krótsza niż przyprostoką tna