prawdopodobieństwo zdarzeń losowych- kolejność n osób aga: 8. Ustawiono w dowolnej kolejności n osób. a) Obliczyć prawdopodobieństwo, że pomiędzy dwiema ustalonymi osobami będzie znajdować się dokładnie r osób. b) Obliczyć prawdopodobieństwo jak w punkcie a), ale dla osób ustawionych w okrąg bardzo proszę o pomoc z wyjaśnieniem

wredulus_pospolitus: oczywiście zakładamy, że r+2 ≤ n

	n!
P(A) =		*(n−2)!*2!
	(r+1)!

jeżeli dodatkowo n ≠ 2r + 2 P(B) = (n−2)!*2! jeżeli natomiast n = 2r + 2 P(B) = (n−2)!

wredulus_pospolitus: poprawka do P(A) oczywiście winno być: P(A) = (n − (r+1))*(n−2)!*2!

wredulus_pospolitus: szczerze mówiąc ... trudno wyjaśnić w momencie w którym nie wiem 'co umiesz' a czego nie umiesz

aga: /czy można prosić o wyjaśnienie/tok rozumowania jak policzono P(A) i co oznacza 2r+2, bo mają to być osoby ustawione w okrąg ale dlaczego akurat taki zapis

wredulus_pospolitus: może zaczniemy od tego, gdy n ≠ 2r+2 ustawiamy kolesia 'A' (pomiędzy nim a kolesiem 'B' ma być dokładnie r osób). Jako, że stoją po okręgu ... to staje on na 1 sposób. Później ustawiamy kolejno 'r' ludzi. Następnie kolesia 'B'. I pozostałych ludzi. wszystkich poza 'A' i 'B' można przestawiać −−− stąd (n−2)!. Ale także można przestawić ze sobą kolesi 'A' i 'B' (raz jeden będzie miał 'za sobą' r osób i 'partnera' raz na odwrót) Czy to jest zrozumiałe?

aga: teraz jest to zrozumiałe

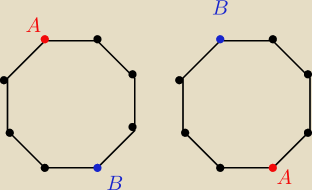
wredulus_pospolitus: To teraz ... gdy mamy n = 2r+2 to będziemy mieli taka sytuację: mamy kolesia 'A' ... następnie r osób, kolesia 'B' i znowu r osób ... i wracamy do kolesia 'A'. W tym momencie nie możemy 'przestawić' ze sobą kolesia A i B, bo dostaniemy to samo: koleś 'A' ma za sobą r osób i kolesia 'B', a także koleś 'B' ma za sobą r osób i kolesia 'A'. Dlatego w tym momencie, mamy tylko (n−2)!

wredulus_pospolitus: Jako, że stoją po okręgu −−− to te dwie sytuacje (rysunek) są dokładnie takie same, po prostu się przesunęli po okręgu o 180^o

aga: Super, już zrozumiałam dzieki wielkie

wredulus_pospolitus: Podejrzewam, że mało kto (może nawet nauczyciel) tego przypadku nie rozpatrzy osobno.

ite: tu są podawane prawdopodobieństwa czy ilości możliwych ustawień?