planimetria
Martyna: Dany jest trójkąt równoramienny, którego podstawa ma długość 20, a ramię 26. Oblicz odległość
przecięcia symetralnych boków tego trójkąta od jego wierzchołków
24 paź 20:11
wredulus_pospolitus:
rysunek wykonany
24 paź 20:15
wredulus_pospolitus:
Co wiemy o punkcie przecięcia się symetralnych w trójkącie
24 paź 20:17
Martyna: Przecinają boki pod kątem prostym i przechodzą przez środek boku.
Rysunek wykonany, próbowałam z trójkątów prostokątnych coś policzyć, ale wychodzi sprzeczność.
24 paź 20:21
wredulus_pospolitus:
Najważniejsza rzecz −−−− przecięcie się symetralnych jest środkiem okręgu OPISANEGO na tymże
trójkącie
24 paź 20:22
Martyna: są środkiem okręgu opisanego na tym trójkącie, czyli odległość do wierzchołka trójkąta to jego
promień
24 paź 20:23
wredulus_pospolitus:
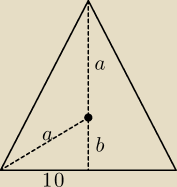
a+b = h =
√262 − 102 = 24
z tw. Pitagorasa:
(24−b)
2 = 10
2 + b
2 −−−> wyznacz 'b'
24 paź 20:23
Martyna: Czy ja dobrze myślę, że mam tam wewnątrz trójkata dwa trójkąty przylegle o wspólnej
przeciwprostokatnej równej tej odległości która szukam?
24 paź 20:28
wredulus_pospolitus:
nie ... szukasz odległości 'b'
24 paź 20:32
Martyna: oK, dziękuję bardzo już wiem, gdzie zrobiłam złe założenie
24 paź 20:32
wredulus_pospolitus:
ach nie ... do wierzchołka ... eeeee ... to nawet nie trzeba Pitagorasa −−− wzór na promień
okręgu opisanego na trójkącie −−− i masz po sprawie
24 paź 20:32
wredulus_pospolitus:
| | abc | |
R = |
| = ... i po sprawie |
| | 4P | |
24 paź 20:33
Martyna: nie miałam jeszcze nic o okręgach, nowa podstawa programowa
24 paź 20:48
wredulus_pospolitus:
no to pitagoras −−− tylko masz wyznaczyć 'a'
24 paź 21:12