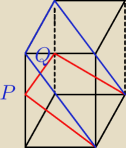
Graniastosłup Iza: Graniastosłup prawidłowy czworokątny przecięto dwiema płaszczyznami i otrzymano przekroje o polach 20 i 8\/13 (rysunek obok). Oblicz objętość tego graniastosłupa, wiedząc, że punkty P i Q są środkami jego krawędzi bocznych.

I'm back: Tam jedt 8√13? 1) zauważamy ze 20 < 8√13 2) V = P_p*H = a²*H 3) wprowadźmy oznaczenie 2b = H 4) z tw. Pitagorasa mamy: a² + b² = 20² a² + (2b)² = (8√13)² Uklad dwóch równań z dwoma niewiadomymi − rozwiazujesz i liczysz objetosc

Iza: A skąd mogę zapisać te twierdzenia Pitagorasa? W sensie skąd wiem, że drugi bok prostokąta zapisujemy jako 20 lub 8√13?

Iza: W odpowiedziach jest, że objętość wynosi 96, a z tego układu wychodzi inaczej

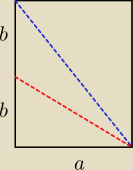
wredulus_pospolitus: 8√13 > 8√9 = 8*3 = 24 > 20 wychodzi inaczej, bo POLA przekrojów mają wartość 20 i 8√3, więc do równań wstawiasz:

	20		8√3
(		)2 i (		)2
	a		a