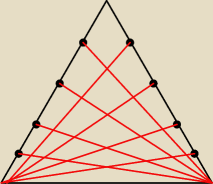
Kombinatoryka Krzysztof: 1. Dana jest krata 10x10. Ile łącznie jest na niej prostokątów? 2. Dany jest trójkąt równoramienny, na ramionach trójkąta obieramy cztery punkty, następnie łączymy je z przeciwległym bokiem (patrz rysunek). Ile jest łącznie wszystkich trójkątów na rysunku?)

wredulus_pospolitus: 1. Jakiś pomysł masz

wredulus_pospolitus: I czy aby na pewno mają to być PROSTOKĄTY a nie przypadkiem czworokąty

wredulus_pospolitus: dobra ... rysunek dotyczy (2) Oki ... to jakie masz pomysły na pierwsze zadanie (które może się wydawać łatwiejszym zadaniem)

Mila: Czy w pierwszym zadaniu jest jakieś ograniczenie? np . boki prostokątów równoległe do boków danego kwadratu? Drugie spróbuję narysować coś tam policzyłam Spróbuj rozwiązać dla dwóch punktów w podobny sposób zaznaczonych jak na Twoim rysunku.

wredulus_pospolitus: @Miluś −−− zapewne boki prostokąta mają być zawarte w kratach

wredulus_pospolitus: @Miluś −−− jak będziesz chciała skonfrontować wyniki to daj znać

a7: 1) 100 kwadratów 1x1 81 kwadratów 2x2 64 kwadraty 3x3 49 kwadratów 4x4 36 kwadratów 5x5 25 kwadratów 6x 6 16 kwadratów 7x7 9 kwadratów 8x8 4 kwadraty 9x9 1 kwadrat 10x10 2x9x10 =180 (90 prostokatów 1x2 plus 90 2x1 (9 w każdej linii)) 2x8x10=160 prostokątów 1x3 2x7x10=140 prostokątów 1x4 2x6x10=120 prostokatów 1x5 2x5x10=100 prostokątów 1x6 2x4x10=80 prostokatów 1x7 2x3x10=60 prostokątów 1x8 2x2x10=40 prostokątów 1x9 2x1x10=20 prostokątów 1x10 2x8x9=144 prstokąty 2x3 2x7x9=126 prostokaty 2x4 2x6x9=108 prostokatów 2x5 2x5x9=90 prostokatów 2x6 2x4x9=72 prostokatów 2x7 2x3x9=54 prstokatów 2x8 2x2x9=36 prostokatów 2x9 2x1x10=20 prostokatów 2x10 2x7x8=112 prostokątów 3x4 2x6x8=96 prostokatów 3x5 2x5x8=80 prostokatów 3x6 2x4x8=64 prostokatów 3x7 2x3x8=48 prostokatów 3x8 2x2x8=32 prostokątów 3x9 2x1x8=16 prostokatów 3x10 2x6x7= 84 prostokatów 4x5 2x5x7 prostokatów 4x6 2x4x7 prostokatów 4x7 2x3x7 prostokatów 4x8 2x2x7 prostokatów 4x9 2x1x7=14 prostokatów 4x10 2x5x6=60 prostokatów 5x6 2x4x6=48 prostokatów 5x7 2x3x6=36 prostokątów 5x8 2x2x6=24 5x9 2x1x6=12 5x10 2x4x5=40 6x7 2x3x5=30 6x8 2x2x5=20 6x9 2x1x5=10 6x10 2x3x4=24 7x8 2x2x4=16 7x9 2x1x4=8 7x10 2x2x3=12 8x9 2x1x3=6 8x10 1x1x2=2 9x10 ________________− 3025

wredulus_pospolitus: @a7 po co to wszystko rozpisywać?

11 2		11 2
	*		= 52*112 = 3025 i po sprawie

Mariusz: a7 a czy to dla kwadratu o rozmiarach nxn nie będzie czasem ∑_k=1ⁿ=k³

a7: Wredulusie− ja zrobiłam na piechotę , Mariuszu − zaraz się zastanowię ale chyba inaczej

a7: @Mariuszu Twój wzór uwzględnia tylko liczbę kwadratów i kwadracików, nie uwazglednia prostokatów 1x2, 2x1, 1x3, 3x1 itd.

Krzysztof: wreduluspospolitus wytłumaczyłbyś proszę tok rozumowania?

Mila: Krzysztof znalazłeś materiały do trójkąta na youtube ?

Mila: Z trójkątem nie piszę, bo jest na youtube. Wystarczy wpisać" How many triangles can you see?" Jest animacja jak liczyć . Po polsku − Ile widzisz trójkątów − jest wzór.

wredulus_pospolitus: Krzysztof −−− masz 11 punktów do wyboru w pionie i 11 w poziomie. Wybierasz 2 w pionie i 2 w poziomie. Kolejność wybrania punktów w pionie nie jest istotna. Analogicznie dla punktów w poziomie

wredulus_pospolitus: Baaardzo podobnie zrobisz ten drugi przykład z trójkątami ... tylko tam jest 'mały haczyk' na który trzeba uważać dodatkowo

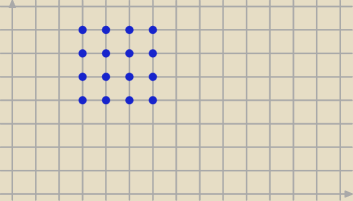
Mila: Coś mi się przywidziało , że w pierwszym zadaniu chodzi o coś takiego tylko 10 x 10.

Mila: Czy interesuje Cię wyprowadzenie za pomocą rekurencji wzoru na liczbę prostokątów w kwadracie.

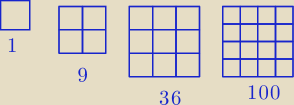
Mila: Liczby prostokątów: a₁=1 a₂=9=1+2³ a₃=36=9+27=1+2³+3³ a₄=100=36+4³=1+2³+3³+4³ a_n=1³+2³+3³+4³+....+10³=(1+2+3+4+5+6+....10)² − wzór z tablic

	n*(n+1)
an=(		)2
	2

	10*11
a10=(		)2=552=50*60+25=3025
	2

a7: Czyli jednak wzór Mariusza jest dobry!

Mila: I wzór wredulusa też prawidłowy, ale jakoś nie mogę sobie wytłumaczyć tak od razu ustalenia wzoru kombinatorycznego jak wredulus. Musiałam trochę policzyć j.w. Podziwiam wytrwałość a7. Załóżmy, że wybiorę punkty z numerami 2 i 3 to wolno mi wybrać 6 i 7 lub 10 i 11 lub 11 i 15 i co ? Arturze, możesz wyjaśnić jak rozumowałeś?

wredulus_pospolitus: @Miliuś ... jak zrozumiałem w jaki szybki sposób zrobić wzór kombinatoryczny? Tak jak napisałem o 21:28. Prostokąt tworzymy jako przecięcie się się dwóch par prostych. Dwie pionowe i dwie poziome. Mamy kratę 10 x 10 ... związku z tym mamy 11 linii pionowych i 11 linii poziomych. Z każdego z tych zestawy wybieramy po dwie linie i w ten sposób otrzymamy prostokąt. Kolejność wyboru linii musimy pominąć, aby wielokrotnie nie zliczać tego samego prostokąta. To tyle. Szczerze mówiąc ... nie wiem jak lepiej / pełniej to wyjaśnić.

Mila: Oświeciłeś mnie Dziękuję. Przepraszam, że niepokoję.

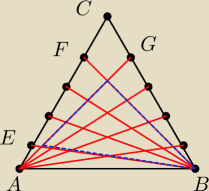
wredulus_pospolitus: Może jeszcze napiszę w jaki sposób bym podszedł do drugiego zdania (nie wiem czy na internetach w taki sposób podchodzili czy nie). 1) Zauważam, że trójkąty będą miały jeden z wierzchołków będący punktem A lub B. Przykładowy (niebieski) trójkąt powstanie jako: I. wybieranie jednego z punktów (A lub B −−− w przykładzie będzie to B) −> ogólnie 2 możliwości, II. wybranie dwóch punktów z odcinka AC (bez możliwości wyboru A), w przykładzie będą to E i F

	5 2
−−−> ogólnie		możliwości

III. wybranie jednego punktu z odcinka BC (bez możliwości wyboru B), w przykładzie będzie to G −−−> ogólnie 5 możliwości. IV. przecięcie odcinków BE, BF i AG daje nam trójkąt. Osobno należy rozpatrzeć sytuację gdy zarówno A jak i B są wierzchołkami trójkąta −−− wtedy wybór ostatniego wierzchołka następuje jako wybór jednego punktu z AC −−−> ogólnie 5 możliwości W efekcie otrzymujemy:

	5 2
2*		*5 + 5 = 5*(5*4 + 1) = 105 trójkątów

Reasumując: Ja nie zastanawiałem się ile jakich figur będzie, tylko spojrzałem w jaki sposób one powstają i co je wszystkie łączy ze sobą

wredulus_pospolitus: no i pomyliłem się w trójkątach −−− jak A i B są wierzchołkami ... to wybieramy jeden z AC (bez A i C) i jeden punkt z BC ( bez B i C) −−−> 4 * 4 i dodatkowo trójkąt ABC −−−> 1

a7: @Milu dziękuję! inną metoda nie umiałabym tego zrobić, a lubię takie zagadki...

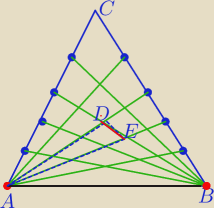
Mila: Liczymy trójkąty o wierzchołku A

	6 2
1) wybieramy 2 ramiona z 6 na		sposobów

2) wybieramy podstawę z: mamy 5 możliwości Zatem z wierzchołka A będzie:

6 2
	*5 =15*5 =75 trójkątów

Liczymy ile jest trójkątów o wierzchołku B . Aby uniknąć dwukrotnego liczenia niektórych Δ to ramiona wybieramy pomijając AB 4)

5 2
	wybór ramion

5) wybór podstawy na 5 sposobów Zatem z wierzchołka B będzie:

5 2
	*5=10*5=50 trójkątów

==================== Razem Liczba trójkątów: 75+50=125 ========= Rozwiązując w podobny sposób jak 14.10 o godzinie 00:08 Otrzymałam wzór : liczba Δ: n³ , gdzie n to liczba odcinków na boku Δ