Czworościan Nalesnior: Kiedy dana ściana czworościanu pada pod kątem prostym względem jego podstawy? Jakie są warunki tego zdarzenia i jak to udowodnić?

I'm back: Wysokość ściany bocznej i wysokość podstawy tworzą kat prosty.

I'm back: Inny sposób spojrzenia na to − − − rzut wierzchołka na podstawę znajduje się na krawędzi tejże podstawy.

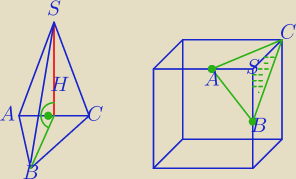
Mila: Dwa przykłady: 1) Ściana ACS jest prostopadła do podstawy ACB 2) Naroże sześcianu : Możesz wybrać SBC jako podstawę czworościanu , wtedy ściana ABS i ściana ACS jest prostopadła SBC.

Nalesnior: Mam zadanie takie by udowodnić, że ściana czworościanu jest prostopadła do podstawy. Zrobiłem bryłę z kartki i zauważyłem, że tak właśnie jest. I nie wiem teraz jak to udowodnić. Chce przeprowadzić prawowity dowód.

I'm back: Ale jak wygląda tenże czworościan.

I'm back: @Milus − drugi przykład (wycięcie z sześcianu) to czworościan foremny w którym żadna ściana nie jest prostopadła do podstawy

I'm back: Dobra. Nie jest foremny, ale nadal − ściana (zaznaczona) nie jest prostopadla

Nalesnior: Żeby to co napisałeś w podpunkcie drugim było prawdą to wpierw muszę udowodnić, że kąt pomiędzy podstawą a ścianą boczną jest prosty.

Nalesnior: Zaraz wysle

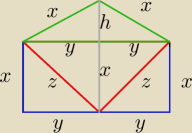
Nalesnior: czerwony − podstawa niebieski − dwa trójkąty przystające tworzące dwie różne ściany boczne zielony ściana boczna Oczywiście jest to względne co jest podstawą a co ścianą boczną(nie zostało powiedziane w poleceniu, ze trójka czerwony jest podstawą), ale tak sobie przyjąłem. Chcę udowodnić że jedna z ścian bocznych jest prostopadła do podstawy, gdyż po zrobieniu bryły z papieru zauważyłem, że jest to możliwe. Chcę to teraz udowodnić matematycznie − algebraicznie a nie dać uzasadnienie polegające na "bo tak mi wyszło". Z góry dzięki za odpowiedź.

Nalesnior: to jest siatka tego czworościanu

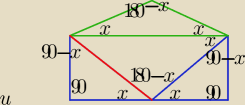
Nalesnior: doszedłem również do takich wymiarów kątów. Może to coś ułatwi

Nalesnior: Sry powinno być 180 − 2x w obu przypadkach

Nalesnior: i x zapomniałem napisać przy kącie czerwony−zielony

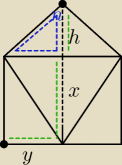
wredulus_pospolitus: Na niebiesko zaznaczyłem jeden z trójkątów prostokątnych, którego przyprostokątne mają długość x i h, przeciwprostokątna natomiast ma długość y Zaznaczyłem też na zielono trzy inne boki, które po złożeniu siatki będą tworzyć trójkąt. Zaznaczone dwa punkty (czarne kropki) oznaczają wierzchołek tegoż czworościanu. Zauważ, że tenże trójkąt ma dokładnie takie same długości boków, Związku z tym są to trójkąty PRZYSTAJĄCE. Związku z tym, ten drugi jest trójkątem prostokątnym o przyprostokątnych długości h i x ... związku z tym pomiędzy nimi mamy kąt prosty. C.N.W.

wredulus_pospolitus: chwila chwila chwila −−− tam niebieski trójkąt ma inaczej boki niż napisałem −−− taka siatka nie daje nam takiego czworościanu o który Ci chodzi ... i to co ja napisałem powyżej pokazuje nam sprzeczność

Nalesnior: właśnie chciałem to napisać bo w twoim oznaczeniu x jest przeciwprostokątną a nie przyprostokątną i chciałem sprawdzić czy jest to jedynie kwestia oznaczeń, lecz jeszcze nie zdążyłem się za to zabrać

Nalesnior: może podobieństwo trójkąta zielonego i czerwonego nam coś ułatwi

Nalesnior: połówki trójkąta czerwonego są przystające do trójkątów niebieskich a połówki trójkąta zielonego są podobne do innych trójkątów To musi prowadzić do jakiegoś rozwiązania

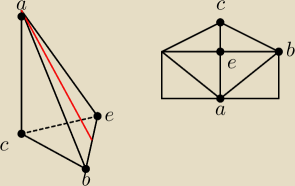
Nalesnior: Po złożeniu siatki tego czworościanu, możemy przepołowić otrzymany czworościan ł i otrzymujemy wtedy inny czworościan. I wysokość ac pada pod kątem prostym. Gdzie: ab = z ae = x ac = ? be = y bc = x ce = h bc = x ab = z czyli żeby wyliczyć ac robimy pitagorasa, więc: x² + (ac)² = z² Wszystko jest git?

Nalesnior: Chyba jest wszystko git ale będzie trzeba parę słów powiedzieć o tym czy ac na pewno pada pod kątem prostym. Ma ktoś pomysł?ł

Mila: I'm back ad wpisu 18:53 mylisz się. To nie jest czworościan foremny. Postaw to odcięte naroże na ścianie BCS ( pudełko zapałek też Ci pomoże).

wredulus_pospolitus: to nie jest dobra siatka −−− z niej nie powstanie czworościan który zaprezentowałeś/−aś

wredulus_pospolitus: @Miluś −−− dlatego zaraz później się poprawiłem ... ale nadal −−− ściany boczne w tamtym przykładzie nie są prostopadłe do podstawy czworościanu (jeżeli podstawą jest ABC, co sugerują oznaczenia)

Nalesnior: @wredulus_pospolitus — siatka niebiescy dobra ale pokazałem ja żeby uzmysłowić wam o jakie punkty mi chodzi.

Nalesnior: *narysowałem

Mila: W czworościanie każda ściana może być podstawą − wg wygody.

wredulus_pospolitus: @Miluś −−− i owszem ... ale jak oznaczasz jeden z wierzchołków jako S (a pozostałem to A,B,C) to samym oznaczeniem sugerujesz gdzie jest wierzchołek

Mila: Jeżeli staniesz na głowie to dalej jesteś Arturem . Pozdrawiam

Nalesnior: Ej ma ktoś pomysł jak udowodnić ze jest tam kat prosty?

wredulus_pospolitus: najpierw narysuj POPRAWNIE siatkę

a7: hej ja się chętnie włączę do dyskusji, ale w końcu jaki jest poprawny rysunek siatki?

Mila: Narysowałabym siatkę, ale nie wiem jaki to czworościan. Może autor zadania napisze treść zadania.

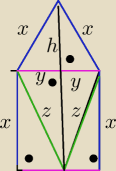
a7: zauważam , że y<x<z h<x z²=x²+y² x²=y²+h² z²=2x²−h² z²=2y²+h²

a7: a która ściana jest prostopadła z modelu "praktycznego"

a7: ?

wredulus_pospolitus: albo inaczej −−− co TUTAJ JEST PODSTAWĄ

Nalesnior: z na z na 2y prostopadła co x na x na 2y

a7: to akurat chyba nie ta ściana, bo h²+x²≠x²

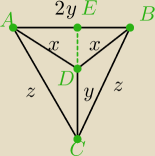
a7: x²=y²+h² czyli ΔEDC jest prostokątny kąt EDC jest prosty

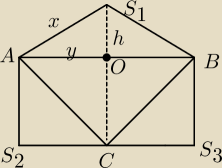
wredulus_pospolitus: @Nalesnior −−− bzduuuura Te dwie ściany (lub jak wolisz − ściana boczna i podstawa) nie są do siebie prostopadłe już wcześniej Ci napisałem w jaki sposób można obalić tą hipotezę Kąt pomiędzy podstawą (ABC) a ścianą boczną (ABS₁) będzie kątem pomiędzy odcinkami OC i OS₁ Zauważmy, że trójkąt AOS₁ jest trójkątem prostokątnym, wynika z niego, że x > y. Zauważmy, że kąt który chcemy wykazać że jest prosty jest kątem w trójkącie OCS₁, długości boków przy tym koncie to odpowiednio h i y ... trzeci bok ma długość równą x ... wiemy że x < y ... więc x NIE MOŻE być przeciwprostokątną ... więc ∡COS₁ <90^o koniec kropka

ite: 21:05 ← Milu jeśli chodzi o treść, to jest bardzo podobna do jednego z zadań z trwającej części korespondencyjnej olimpiady. P.S. Pomysł na wredulusa stojącego na głowie przy odwróconym czworościanie bardzo mi się spodobał : )

Mila: Dziękuję ite, spojrzę jutro do tej olimpiady.

Nalesnior: @werdulus_pospolitus−−−bzdurą jest to co ty piszesz raz mówisz, że x>y (co jest prawdą) po czym w kolejnym zdaniu piszesz, że x<y zastanów się

wredulus_pospolitus: Nalesior −−− zwróć uwagę że znowu pomyliłem długości boków. Przeanalizuj na spokojnie a zobaczysz, że ta ściana NIE MOŻE być prostopadła. Co więcej −−− łatwo pokazać, że ∡OS₁C będzie kątem prostym ... co oznacza, że ∡COS₁ nie może być kątem prostym

wredulus_pospolitus: Poprawiając to co wtedy napisałem: @Nalesnior −−− bzduuuura Te dwie ściany (lub jak wolisz − ściana boczna i podstawa) nie są do siebie prostopadłe już wcześniej Ci napisałem w jaki sposób można obalić tą hipotezę Kąt pomiędzy podstawą (ABC) a ścianą boczną (ABS1) będzie kątem pomiędzy odcinkami OC i OS1 Zauważmy, że trójkąt AOS1 jest trójkątem prostokątnym, wynika z niego, że x > y. Zauważmy, że kąt który chcemy wykazać że jest prosty jest kątem w trójkącie OCS1, długości boków przy tym koncie to odpowiednio h i x ... trzeci bok ma długość równą y ... wiemy że x > y ... więc y NIE MOŻE być przeciwprostokątną ... więc ∡COS1 <90o koniec kropka *na czerwono jest to co poprawiłem błąd polegał na tym, że pisząc to pisałem tak jakby |OC| = y a nie = x i stąd ten błąd.