Trójkąt Gucio: W trójkącie ABC mamy dane: /AC/=3 /BC/=4 /AB/=6. Punkt D należący do odcinka AB dzieli go w ten sposób, że długość odcinka DB jest 2 razy większa niż długość odcinka AD. Wówczas długość odcinka CD jest równa: a)4 b)√11/3 c)3 d)√10/3

an: Korzystając z twierdzenia Carnota na długość środkowej

	1
d=		√2⇒a2+2b2−c2
	2

CD=√10/3

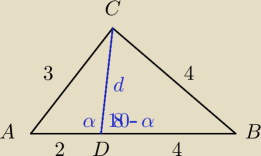
Saizou : Tak jak pisze an skorzystajmy z tw. cosinusów 9=4+d²−4dcosα

	1
16 = 16 +d2−8dcos(180−α) →8=8+		d2 +4dcos(α)
	2

===============+

	3
17 = 12 +		d2
	2

10 = 3d² d = √10/3

Mila: Korzystając z tw. Stewarta: 3²*4+4²*2=6*(d²+2*4)

	10
d2=
	3

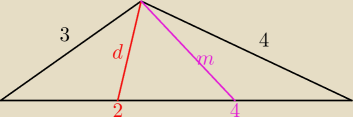
an: Ja to chciałem j/n, ale Saizou jest bardziej zgodne z programem d=1/2√2*3²+2*m²−4² ⇒4d²=2+2m² m=1/2√2*d²+2*4²−4² ⇒2m²=d²+8

	10
d=√
	3

Mila: