Sinus Natec: sin²x − 5sinx + 6<0 Wyznacz zbiór nierówności, wyszło mi że zbiór pusty.

wredulus_pospolitus: zauważmy, że: sin²x ≥ 0 w takim razie: sin²x + 6 ≥ 6 natomiast −5sinx ≥ −5 związku z tym sin²x − 5x + 6 ≥ −5 + 6 = 1 więc tak ... rozwiązaniem będzie zbiór pusty

K8: albo tak sin²x−5sinx+6<0 (sinx−2)(sinx−3) <0 sinx=2 −−sprzeczość v sinx= 3 −− sprzeczność x∊∅

wredulus_pospolitus: K8 −−− Twoje rozwiązanie byłoby dobre gdyby to było równanie. Przy nierówności jeszcze konieczny jest komentarz

K8:

wredulus_pospolitus: @K8 −−− co Ty tutaj narysowałeś

K8: mordeczkę

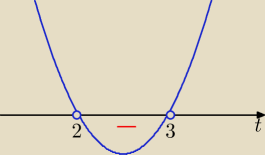
K8: sinx=t t∊<−1,1> (t−2)(t−3)<0 ⇒ t∊(2,3) to sinx∊(2,3) −− sprzeczne teraz pasuje ?