prawdopodobieństwo anonim123: Spośród cyfr 1, 2, ..., 9 losujemy kolejno bez zwracania trzy cyfry c1, c2, c3 i tworzymy z nich liczbę o zapisie dziesiętnym c1,c2,c3 czyli tutaj nie ma być żadnych liczb z przecinkiem?

chichi: 9,7,8 widziałaś kiedyś taką liczbę?

a7: nie, chodzi o to że wylosujemy np. 123 123 124 125 126 127 128 129 213 214 215 216 217 218 219 312 314 315 316 317 318 319 412 413 415 416 417 418 419 512 513 514.............

anonim123: Dalszą część ile różnych liczb mniejszych od 555 można otrzymać? Tak tam przy zapisie dziesiętnym nie miało być żadnych przecinków czy można by to rozwiązać tak że biorę najmniejszą liczbę 111 liczę wszystkie liczby pomiędzy 111 a 222 to jest 1*9*9 i podobnie dalej i mam 81*5 jako wynik?

chichi: a jak utworzysz liczbę 111, skoro losujemy BEZ ZWRACANIA

anonim123: Zaraz poprawię

anonim123: Czyli dla jedynki z przodu będzie 72 i teraz mnożę razy 4 i dla piątki z przodu mam 5*4*3 i Ostatecznie 72*4*60?

anonim123: ?

I'm back: .

I'm back: Skąd te liczby? 4*8*7 + 1*4*7 =... To jest Twoje rozwiązanie w przypadku gdy cyfry nie mogą się powtarzać.

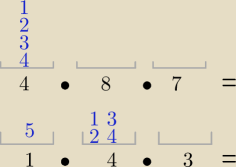
K8: 1/ wszystkie zaczynające się na {1,2,3,4} na pierwszym miejscu jedna z czterech na drugim miejscu jedna ze wszystkich 9 oprócz tej pierwszej na trzecim miejscu jedna z 9 oprócz pierwszej i drugiej jest ich 4*8*7= ........ 2/ zaczynające się na 5 na drugim miejscu jedna z {1,2,3,4} na trzecim miejscu jedna już tylko z trzech <5 jest ich 1*4*3=... Razem: 4*8*7+1*4*3 = takich liczb <555

K8: poprawiam : 2/na trzecim miejscu już tylko jedna z 7 ( bo bez 5 i bez jednej na drugim) jest ich 1*4*7 Razem 4*7*8+1*4*7=.....

anonim123: Dziękuję

anonim123: A to da się zrobić korzystając ze wzoru na wariacje bez powtórzeń?