Pole okręgu opisanego na trójkącie Julia: W trójkącie równobocznym ABC o obwodzie 6 na boku AC wybrano punkt P taki, że |AP|\|PC|=1\5 Oblicz pole koła opisanego na trójkącie APB.

I'm back: 1) wyznacz |AC| 2) wyznacz |AP| 3) wyznacz |PB| z tw. cosinusow 4) liczysz promień z odpowiedniego wzoru

K8:

	1
12b=2 ⇒ b=
	6

	√3
|PD|=b√3=
	6

	1
|DB|= 2−		=........
	6

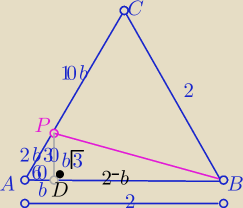
Z tw. Pitagorasa w ΔDBP :

	√31
|BP|= ............=
	3

z tw. sinusów w ΔAPB

	|BP|
2R=		=................
	sin60o

R=......... R²=........ P_k=πR²=.........

Julia: Jaki zastosować wzór na promień ?

I'm back: K8 zapisał wszystkie wzory − 'paczaj'

pavlonek: Dlaczego bok podzieliliśmy na 12 części? i skąd znamy kąty trójkąta ADP?

on:

	2b
		=1:5
	10b