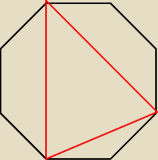
pole Michał: Oblicz stosunek pola trójkąta do pola ośmiokąta

chichi:

1   [a(1 + √2)]2sin(π/4) 2		1
	=		(2 + √2)
2a2(1 + √2)		8

Mariusz: chichi a jakiś komentarz do tego Jeśli chodzi o pole ośmiokąta to zakładając że ośmiokąt jest foremny można podzielić go na trójkąty równoramienne

	2π
Ponadto wiedząc że kąt między ramionami to		, n=8
	n

możemy skorzystać ze wzoru na pole z sinusem Długość ramienia można policzyć z trygonometrii

	π		a   2
sin(		)=
	n		R

	π		a
Rsin(		)=
	n		2

	a
R=
	π   2sin( )   n

	1		a		a		2π
P=n*		*(		)*(		)*sin(		)
	2		π   2sin( )   n		π   2sin( )   n		n

	n	a2		π		π
P=			*2sin(		)cos(		)
	2	π   4sin2( )   n		n		n

	n		π   cos( )   n
P=		a2
	4		π   sin( )   n

Wstawiając do powyższego wzoru na pole n=8 dostaniemy pole ośmiokąta foremnego a jak dostać pole tego trójkąta którego boki zaznaczono na czerwono ?

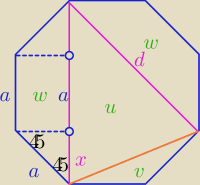
chichi: @Mariusz

	a√2
x =		, d = a + 2x = a(1 + √2)
	2

	a√2
S = 2w + u + v, 2w = [a + 1(1+√2)]
	2

	1		π		1		3π
u =		[a(1 + √2)]2sin(		), v =		a2sin(		)
	2		4		2		4

jakby coś jeszcze było niejasne to pytaj

chichi: 2w = ... tam przed okrągłym nawiasem winno być 'a' zamiast 1 oczywiście

Mariusz: To ja chciałem policzyć długości boków tego trójkąta z tw cosinusów ale to na razie był tylko pomysł Pomysł ten mógłby być dobry bo z tego co widzę to do policzenia długości jednego z boków wystarczy raz zastosować tw cosinusów a do policzenia długości boku oznaczonego u ciebie jako d można dwukrotnie zastosować tw cosinusów Twój wpis z 6 paź 2022 18:03 powinien być zrozumiały

chichi: ile ludzi tyle pomysłów Mariusz, ja miałem taki 1 pomysł i udało się szybko

Mariusz: Czy ten trójkąt to czasami nie jest trójkątem równoramiennym gdzie kąt między ramionami jest kątem wpisanym w okrąg opisany na tym ośmiokącie

	π
Wtedy miara kąta będzie wynosić		, długość podstawy z twierdzenia cosinusów
	8

Długość wysokości można policzyć z wartości funkcji trygonometrycznej a pole ze wzoru z wysokością

chichi: o którym trójkącie mówisz?

Mariusz: Tym zaznaczonym na czerwono w pierwszym wpisie tego wątku

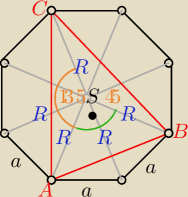
K8: Można też tak :

	1
Pośm. = 8*		R2sin45o = 2R2√2
	2

P_ΔABC = P_ΔABS+ 2P_ΔACS

	1		1
PΔABC=		R2+2*		R2*sin135o
	2		2

	1
PABC=		R2(1+√2)
	2

PΔABC		1
	=		(2+√2)
Pośm		8

============= i po ptokach Rozwiazanie chichi piękne ....w swojej prostocie

chichi: no sam wzór na 'u' z 18:03 to pokazuje − oczywiście, że jest równoramienny. trapezy o polu 'w' są przystające, co implikuje, że trójkąt jest równoramienny

chichi: super

chichi: sprawdź proszę P_ośm.

chichi: przepraszam, tam bazujesz na promieniu, a nie dłg. boku − moje niedopatrzenie

K8:

chichi: a tak jeszcze przy okazji, to porównując wyprowadzone przez nas wzory na pola mamy od razu wzór na promień okręgu opisanego na tej figurze:

	a
2R2√2 = 2a2(1 + √2) ⇒ R =		√4 + 2√2
	2

Mariusz:

	2π
α = π −
	n

	2π
v2=a2+a2−2*a*a*cos(π −		)
	n

	2π
v2=2a2+2a2cos(		)
	n

	2π
v2=2a2(1+cos(		))
	n

	π		π		π		π
v2=2a2(cos2(		)+sin2(		)+cos2(		)+sin2(		))
	n		n		n		n

	π
v2=2a2*2cos2(		)
	n

	π
v2=4a2cos2(		)
	n

	π
v=2acos(		)
	n

Teraz gdyby nawet był to trójkąt równoramienny gdzie miara kąta między ramionami jest równa mierze kąta wpisanego w okrąg opisany na ośmiokącie to i tak trzeba by znać miarę kąta środkowego aby móc z tego skorzystać

	4π
Miara kąta środkowego opartego na tym samym łuku co kąta wpisanego to
	n

	2π
Kąt między ramionami trójkąta jest kątem wpisanym więc ma miarę
	n

	π
v=2acos(		)
	n

Jeżeli w tym trójkącie poprowadzimy wysokość to podzieli ona nam zarówno podstawę jak i kąt między ramionami na połowę Z wartości funkcji trygonometrycznych (tangens lub jeśli znamy to nieco lepiej cotangens) obliczamy wysokość

	π		h
ctg(		)=
	n		π   a*cos( )   n

	π		π
h=a*cos(		)ctg(		)
	n		n

	π   cos2( )   n
h=a
	π   sin( )   n

	1		π   cos( )3   n
P=		a2
	2		π   sin( )   n

Aby obliczyć długość boku zaznaczonego u ciebie jako d z twierdzenia cosinusów to trzeba by znać miarę kąta

Mariusz: Zdaje się że zgubiłem dwójkę podczas liczenia pola Rozwiązanie podane przeze mnie jest jednak nieco bardziej ogólne