Okrąg opisany na trójkącie KAsia: W trójkącie równoramiennym ABC o podstawie AB środkowe poprowadzone z wierzchołków A i B przecinają się pod kątem prostym w punkcie P oraz \AP\ = 6. Oblicz długość okręgu opisanego na tym trójkącie.

I'm back: 1) znając |AP| znamy |BP| 2) więc możemy obliczyć |AB| 3) możemy też policzyć pole ΔABP co w konsekwencji daje nam pole ΔABC 4) w takim razie znamy h_ΔABC 5) w takim razie znamy |AC| = |BC| 6) korzystamy z odpowiedniego wzoru do wyznaczenia promień okregu opisanego na trójkącie ABC

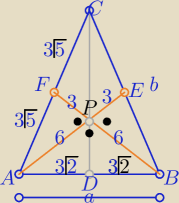
K8: Aż taka "litania" nie jest potrzebna wystarczy taka; Środkowe trójkąta dzielą się w stosunku 2:1 licząc od wierzchołka i dzielą trójkąt na sześć trójkątów o równych polach P_ΔAFP=9 to P_ΔABC= 6*9=54 z tw. Pitagorasa |AF|=√6²+3²= 3√5 to b= 6√5 i a= 6√2

	a*b*b
R=		=........
	4P

R=5√2 P_k=πR² = 50π