Obliczenie długości odcinka
Rafal:
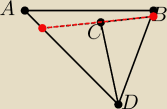
Proszę o pomoc. Znam 4 punkty na układzie współrzędnych
A (−3.66;0)
B (3.66;0)
C (0.5;−0.1)
D (0.7;−7)
Chciałbym obliczyć długość (czerwonej linii) która jest prostopadła do odcinka CD. Przechodzi
przez punkt C. Jej początek jest na odcinku AD i koniec na odcinku BD.
2 paź 18:40
mat:
1/ piszesz równanie prostejCB
2/ piszesz równanie prostej AD
3/ rozwiązujesz układ równań tych prostych
otrzymując punkt E
4/ liczycz długość |EB|=..
i to wszystko
2 paź 19:05
Rafal: Dziękuję za szybką odpowiedź.
Niestety, ale punkt końcowy odcinka (czerwonego) nie jest w punkcie B tylko na odcinku BD.
2 paź 19:25
wmboczek: z drobną modyfikacją przejdzie
1) prosta AD
2) prosta BD
3) prosta CD
4) prostopadła co CD przez C
5) przecięcie 4) z 1) i 4) z 2)
6) odl między pkt z 6)
2 paź 19:30
Rafal:
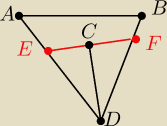
Poprawiłem rysunek aby był czytelniejszy
|CD| jest prostopadłe do |EF|
2 paź 19:31
Rafal: Dziękuję. Czy mógłbym poprosić o pełne obliczenia?
1) prosta AD
2) prosta BD
3) prosta CD
4) prostopadła co CD przez C
5) przecięcie 4) z 1) i 4) z 2)
6) odl między pkt z 6)
2 paź 19:38
mat:
Kto Ci dał takie "koszmarne" współrzędne ?
2 paź 20:15
Rafal: Czy mogę poprosić o wzory i obliczę/podstawię dane samemu?
2 paź 20:36
wredulus_pospolitus:
nie wiesz jak się wyznacza wzór prostej mając współrzędne dwóch punktów
2 paź 20:38
Rafal: Wzór prostej potrafię ale mam problemy z poniższymi wzorami:
4) prostopadła co CD przez C
5) przecięcie 4) z 1) i 4) z 2)
6) odl między pkt z 6)
2 paź 20:41
I'm back:
(4) dwie proste są prostopadle gdy jaki warunek zachodzi (związany z ich współczynnikami
kierunowymi)?
(5) przecięcia będą po prostu rozwiązaniami rownan.
f(x) = g(x) daje Ci współrzędna x'osowa Pu ktu przecięcia się tych dwóch prostych
2 paź 21:29
Rafal: (4) dwie proste są prostopadle gdy jaki warunek zachodzi (związany z ich współczynnikami
kierunowymi)?
Nie ma warunku. Po prostu jest taka infiormacja.
(5) przecięcia będą po prostu rozwiązaniami rownan.
f(x) = g(x) daje Ci współrzędna x'osowa Pu ktu przecięcia się tych dwóch prostych
Nie rozumiem tego. Czy możesz rozwinąć?
3 paź 08:05
I'm back:
Ja pierdziele. To było pytanie do Ciebie − ZNAJDŹ WARUNEK JAKI SPELNIC MUSZĄ DWIE PROSTE ABY
BYŁY ONE DO SIEBIE PROSTOPADLE
To nie było pytanie czy jest jakiś warunek w treści zadania.
Widzę że u Ciebie mocno na bakier z jakąkolwiek teoria.
3 paź 08:12
I'm back:
Powiedźmy ze f(x) = − x + 1, g(x) = 2x + 7
f(x) = g(x) − − − > − x+1 = 2x+7 − − − > 3x = 6 − − − > x = 2 − − − > f(2) = − 2 +1 = − 1
Punkt przecięcia to P(2, − 1)
Robisz analogicznie dla swoich prostych
3 paź 08:22
3 paź 20:23
a7: w razie pytań chętnie wyjaśnię co się ską wzięło... i jak wszytsko policzyć
3 paź 23:20
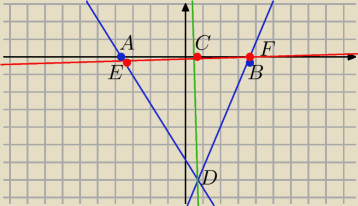1.równanie prostej CD
A (−3.66;0)
B (3.66;0)
C (0.5;−0.1)
D (0.7;−7)
y=ax+b
−0,1=a*0,5+b & −7=a*0,7+b