Siemano 0_0: Jak znaleźć dziedzinę funkcji? wiem jak to się robi, tylko mam problem z tym przykładem i liczę na tłumaczenie

	2
f(x) = log0,8|x − 1| −
	x

z góry pozdrawiam

chichi: x ≠ 0 ∧ |x − 1| > 0 ⇔ x ∊ R \ {0,1}, D_f = R \ {0,1}

0_0: Dzięki, ale to nie może być takie proste

0_0: ponieważ całe to wyrażenie musi być większe od zera, nie tylko wartość bezwzględna

0_0: chodzi mi o to:

	2
|x − 1| −		> 0
	x

chichi: jeżeli miałoby tak być to funkcja f powinna być dana wzorem:

	2
f(x) = log0.8(|x − 1| −		), niestety Twój zapis jest inny, zatem dziedzina jest taka
	x

jak podałem.

0_0: a to przepraszam, to ma być w nawiasie

chichi: Jeśli naprawisz wzór funkcji jak podałem o 19:58 wówczas trzeba będzie rozpatrzyć:

	2
|x − 1| −		> 0 ∧ x ≠ 0
	x

Gdybyś miał problem z rozwiązaniem tej nierówności to pisz, ale jest to banalnie proste

0_0: no mam problem bo 3 różne żeczy mi wyszły, a tam zrobiłem błąd z minusem ma być:

	2
|x + 1| −		> 0
	x

↗−−− plus tu

chichi: graficznie ładnie wyjdzie, jak nie to rozpatrz dwa przypadki :

	⎧	x−1, gdy x≥1
|x−1|=	⎨
	⎩	1−x, gdy x<1

0_0: dobra, czyli mam tak zrobić?

	2		2
x + 1 −		> 0 ⋁ x + 1 +		< 0
	x		x

chichi: formalnie powinna być alternatywa dwóch układów równań nierówności ze względu na rozpatrywane przydziały dla x, ale weź sobie przekrój z odpowiadającymi przedziałami na których rozpatrywane sa dane nierówności pod koniec i będzie ok.

Filip: chichi a ty nadal siedzisz na tym forum matematycznym zamiast robić coś w swoim w marnym życiu

0_0: Mam, tak zrobiłem:

	2		2
x + 1 −		> 0 ∨ x + 1 +		< 0 / *x2
	x		x

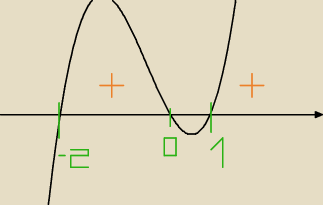
x³ + x² − 2x > 0 ∨ x³ + x² + 2x < 0 x(x² + x − 2) > 0 ∨ x(x² + x + 2) < 0 (rys.) x(x−1)(x+2) > 0 ⋁ x∊ (−∞,0) x∊ (−2,0)∪(1,∞), x ≠ 0 Df=(−∞,0)∪(1,∞) Pozdrawiam, z fartem

K8:

	2
D : |x−1|>
	x

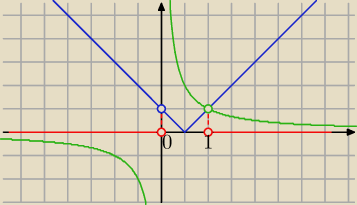
D : x∊(−∞, 0) U (1,∞) i po ptokach