Zadanie Xyz: Punkty A(0,5), B(2,6) sa wierzcholkami trojkata prostokątnego ABC, nato−miast punkt C lezy na prostej o równaniu y=x trzeba obliczyć ile i jakie współrzędna ma wierzchołek c

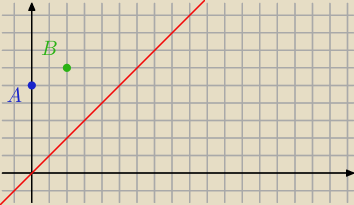
wredulus_pospolitus: 0) rysunek A. możliwość "1" AB i BC są przyprostokątnymi 1) wyznaczasz prostą zawierającą AB 2) wyznacza prostopadłą do AB przechodzącą przez B 3) punkt przecięcia tejże prostej z prostą y=x daje Ci współrzędne punktu C B. możliwość "2" AB i AC są przyprostokątnymi 1) wyznaczasz prostą zawierającą AB 2) wyznacza prostopadłą do AB przechodzącą przez A 3) punkt przecięcia tejże prostej z prostą y=x daje Ci współrzędne punktu C C. możliwość "3" AB jest przeciwprostokątną (czyli AC i BC to przyprostokątne) tą możliwość (patrząc na rysunek) będzie trzeba obalić ... tylko jak ... hmmm ... hmmm indeed popatrz na rysunek i zastanów się co wiemy o długości przeciwprostokątnej w porównaniu do przyprostokątnych ... i jak to wykorzystać w tym zadaniu

Emil: Skorzystaj z warunku prostopadłości wektorów i po ptokach

Mariusz: Arturze może zacznij od sprawdzenia iloczynu współczynników kierunkowych A=(0,5) B=(2,6) C=(p,p) Warunek na to aby proste y=a₁x+b₁ oraz y=a₂x+b₂ były prostopadłe to a₁a₂=−1

	p−5
lAC: y =		x+5
	p

	p−6
lBC: y =		(x−2)+6
	p−2

p−5	p−6
		=−1
p	p−2

−p(p−2)=(p−5)(p−6) −p²+2p=p²−11p+30 2p²−13p+30=0 Δ=169−4*2*30 Δ=169−240 Δ=−71 < 0 p ∉ ℛ Co do wektorów to nie wiadomo czy znają to pojęcie Jeżeli wolimy postać ogólną prostej to warunek na prostopadłość prostych wygląda bardzo podobnie do wzoru na cosinus różnicy

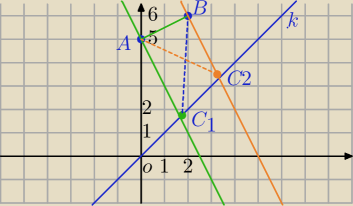Mila: 1) Wykorzystujemy prostopadłość AC lub BC do prostej AB

	1
AB: y=		x+5
	2

Prostopadła do AB i przechodząca przez punkt A=(0,5) y=−2x+b y=−2x+5 C=(x,x) Punkt przecięcia z prostą k: y=x −2x+5=x

	5
x=
	3

	5		5
C1=(		,		)
	3		3

lub Prostopadła do AB i przechodząca przez punkt B=(2,6) y=−2x+b i 6=−2*2+b BC₂ : y=−2x+10 −2x+10=x

	10
x=
	3

	10		10
C2=(		,		)
	3		3

II AB^→[2,1] AC⊥AB [x,x−5] o [2,1]=0 2x+x−5=0

	5		5		5
x=		⇔C1=(		,		)
	3		3		3

lub BC⊥AB [x−2,x−6] o[2,1]=0 2x−4+x−6=0

	10
x=
	3

	10		10
C2=(		,		)
	3		3