Wzór taylora cezar: Muszę wyprowadzić z następującej funkcji f(x)=¹₈(sin(3x)−sin(−5x)+4) wzór taylora do 3 rzędu wokól punkt x = 0. Chciałbym prosić o pomoc w analize błędu. Ponieważ wynik, który uzyskuje to jest ¹₂+x+x², natomiast wynik jaki powinienem otrzymać to ¹₂+2x². Oto jakie obliczenia poczyniłem. 1.Najpierw licze pierwszą pochodną tej funkcji f(x)=¹₈(sin(3x)−sin(−5x)+4) Pochodna pierwsza z tej funkcji to: f'(x) = ^{3cos(3x)+5cos(5x)}₈ 2.Teraz licze drugą pochodną z funkcji f'(x) = ^{3cos(3x)+5cos(5x)}₈ f''(x) = ^{−9sin(3x)−25sin(5x)}₈ 3.I na koniec licze trzecią pochodną z tego f''(x) = ^{−9sin(3x)−25sin(5x)}₈ f'''(x) = ^{−27cos(3x)−125cos(5x)}₈ I teraz wyprowadzam wzór Taylora f(x) = ¹₂+ 1(x−0)+(x−0)²+(^{−27sin(3c_x−125sin(5_x)}₄₈) = ¹₂+x+x²+(^{−27sin(3c_x−125sin(5_x)}₄₈). To jest mój wynik ¹₂+x+x²+(^{−27sin(3c_x−125sin(5_x)}₄₈), a powinno wyjść ¹₂+2x². Wydaje mi się że w tym wyniku co ja uzyskałem to to (^{−27sin(3c_x−125sin(5_x)}₄₈) powinno zostać. Tak przynajmniej widziałem na yt https://www.youtube.com/watch?v=tEYcXjSEBU4. To jaki w końcu będzie ostateczny wynik

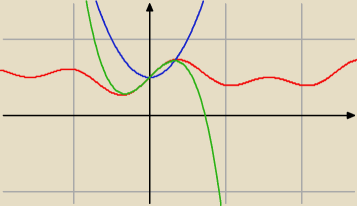
wredulus_pospolitus: Błędnie jest zarówno Ty jak i odpowiedź. Na rysunku masz: 1/8 * (sin(3x) + sin(5x) + 4) 2x² + 1/2 1/2 + x + −19/6 * x³ Jak widzisz −−− zielony wykres 'nachodzi' na czerwony

	f''(0)		f'''(0)
f(x) = f(0) + f'(0)*x +		*x2 +		x3
	2		6

druga sprawa:

	1
f(0) =		okey
	2

f'(0) = 1 f''(0) = 0

	152
f'''(0) = −		= −19
	8

Przy okazji

cezar: Słyszałem że jeśli trzeba jakąś funkcje rozwinąć w szereg Taylora ale jest w niej punkt x₀ = 0 to trzeba zastosować specjalny typ wzoru Taylora czyli wzór maclaurina. Rozumiem że twoje rozwiązanie jest oparte właśnie na wzorze maclaurina ?

wredulus_pospolitus: po prostu nie zapisałem (x−0)ⁿ ... tylko od razu xⁿ ... to cała różnica

cezar: Dzięki