Udowadnianie stosunku pól
KAsia:
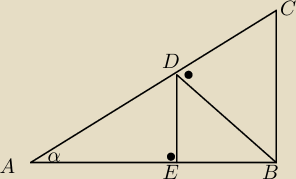
Dany jest trójkąt prostokątny ABC.
Wykaż, że stosunek pól trójkątów:
a) BDC i ABC jest równy sin
2α,
b) AED i ABC jest równy cos
4α.
16 wrz 15:50
Mila:
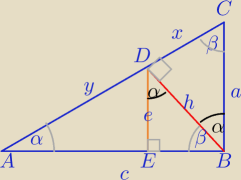
a)
| | x | | h | |
= |
| * |
| =sinα*sinα=sin2α |
| | a | | c | |
b) zrobisz sama?
16 wrz 17:06
KAsia: Mogłabyś rozpisać proszę też podpunkt b) bo nie mogę do tego dojść
16 wrz 17:18
Mila:
Podpowiedź:
Za godzinę będę na forum.
16 wrz 18:12
KAsia: Niestety dalej nie wiem jak dojść do odpowiedzi
16 wrz 19:30
Mila:
| | PAED | | | | y*e*cosα | |
1) m= |
| = |
| = |
| |
| | PΔABC | | | | a*c | |
2)
| | e | |
W ΔDEB: cosα= |
| ⇔e=h*cosα |
| | h | |
3)
| | y*e*cosα | | y*h*cosα*cosα | |
m= |
| = |
| ⇔ |
| | a*c | | a*c | |
| | h | | y | |
m=cos2α* |
| * |
| =cos2α*cosα*cosα |
| | a | | c | |
m=cos4α
========
16 wrz 20:24
KAsia: Dziękuję bardzo za pomoc

A czy mogłabyś pomóc mi jeszcze w tym zadaniu?
Udowodnij, że dla dowolnej liczby naturalnej
n ≥ 3 istnieje liczba pierwsza p taka, że:
n < p < n!
Wskazówka. Rozpatrz liczbę n! − 1.
16 wrz 20:38
ABC:
no więc rozpatrz ją i zauważ że skoro n≥3, to n!−1 >1 co jest kluczowe ,
bo posiada wtedy liczba n!−1 dzielnik pierwszy p.
Załóż że p≤n i dojdź do sprzeczności (z tym że p dzieli wówczas 1, bo..... )
zatem p>n i oczywiście z określenia p<n!, co należało pokazać
16 wrz 22:27
Eta:
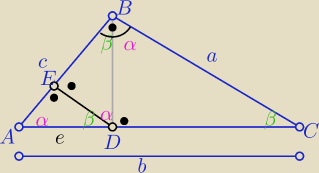
| | a | |
a) ΔBDC∼ΔABC z cechy (kk) w skali k= |
| |
| | b | |
| | PBDC | | a2 | | a | |
m= |
| =k2= |
| i w Δ ABC sinα= |
| |
| | PABC | | b2 | | b | |
to m= sin
2α
==========
| | e | |
b) ΔADE ∼ΔABC z cechy (kk) w skali k= |
| |
| | b | |
| | PADE | | e2 | | c2 | |
to m= |
| = k2 = |
| |* |
| |
| | PABC | | b2 | | c2 | |
| | e2 | | c2 | | e | | c | |
m= |
| * |
| oraz w ΔADB cosα= |
| i w ΔABC cosα= |
| |
| | c2 | | b2 | | c | | b | |
to
m= cos
4α
=========
i po ptokach

17 wrz 14:46
Mila:
Ad. 20:38
Twierdzenie Czebyszewa .
[N[Dla każdej liczby naturalnej n > 1
istnieje liczba pierwsza p taka, że n < p < 2n.]]
Przy założeniu: n≥3 i tw. Czebyszewa
n<p<2n≤n!
17 wrz 20:14
Mariusz :
Eto też pomyślałem aby spróbować tutaj wykorzystać podobieństwo trójkątów
Milu dlaczego sugerujesz błędną wymowę nazwiska tego matematyka
17 wrz 20:19
ABC: Mariusz a jaka jest prawidłowa wymowa?
17 wrz 20:56
ABC:
Mila ale dowód tego twierdzenia to nie w kij dmuchał , choć widziałem jeden elementarny ale za
to długi dosyć

17 wrz 20:58
Mariusz :
ABC nie wiesz was jeszcze uczyli rosyjskiego
To ja mógłbym nie wiedzieć (choć akurat tutaj wiem) bo ja już za młody jestem aby mnie uczyli
Cziebyszow − pierwsza sylaba miękko , ostatnia zaczyna się spółgłoską twardą
więc zamiast io czyta się o, akcent jest na ostatnią samogłoskę
17 wrz 21:12
ABC:
Пафнутий Львович Чебышёв − tak to wygląda w cyrylicy
uczyłem się 8 lat ale
nie jestem specjalistą filologii rosyjskiej, może jakiś się wypowie na temat wymowy prawidłowej

17 wrz 21:33
17 wrz 21:38
ite:
Skrótowo ale skutecznie:
W nazwisku występuje samogłoska wymawiana jako "o" i to słychać w filmie.
W tytule filmu nazwisko jest zapisane za pomocą litery "e", w napisach na początku filmu
zapisano je za pomocą "ё".
Do pierwszej połowy XX w. (a więc również w tym czasie wtedy gdy żył Pafnucy Lwowicz) używano
tylko jednej litery → "e". Dzisiaj często nadal używa się jej tam, gdzie mogłoby być "ё". U
nas powoduje to zamieszanie i różnice między wymową a transliteracją.
17 wrz 22:48
ite:
Mariusz języka obcego można się uczyć w każdym wieku, nie jesteś na to za młody.
Nie przejmuj się tak wiekiem (ani swoim ani innych).
17 wrz 23:15
 Dany jest trójkąt prostokątny ABC.
Wykaż, że stosunek pól trójkątów:
a) BDC i ABC jest równy sin2α,
b) AED i ABC jest równy cos4α.
Dany jest trójkąt prostokątny ABC.
Wykaż, że stosunek pól trójkątów:
a) BDC i ABC jest równy sin2α,
b) AED i ABC jest równy cos4α.

 A czy mogłabyś pomóc mi jeszcze w tym zadaniu?
Udowodnij, że dla dowolnej liczby naturalnej
n ≥ 3 istnieje liczba pierwsza p taka, że:
n < p < n!
Wskazówka. Rozpatrz liczbę n! − 1.
A czy mogłabyś pomóc mi jeszcze w tym zadaniu?
Udowodnij, że dla dowolnej liczby naturalnej
n ≥ 3 istnieje liczba pierwsza p taka, że:
n < p < n!
Wskazówka. Rozpatrz liczbę n! − 1.




