sześciokąt lew17: Niech ω₁ i ω₂ będą okręgami o promieniu odpowiednio 6 i 8, o wspólnym środku w O. Trzy różne równo rozmieszczone punkty, A, B, C leżą na ω₂. Niech boki trójkąta ABC przecinają się z ω₁ w X, Y, Z, P, Q, R. Oblicz pole sześciokąta wypukłego XYZPQR.

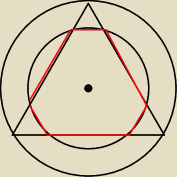
wredulus_pospolitus: zauważ, że małe trójkąty będą trójkątami równobocznymi o h = (8−6) = 2, stąd wyznaczasz ich

	3
bok, liczysz pole ... odejmujesz od pola dużego trójkąta (którego H =		*8) i gotowe
	2

0_0: Ale ESSA

lew17: Czemu h = (8−6) = 2 ?

I'm back: Patrz jakie okręgu mają promień. Zauważ czym jest wysokość dużego trójkąta, a czym jest wysokość małego trójkąta.

lew17: Nadal nie rozumiem czemu h=8−6 to wysokość. Ten trójkąt na dole ma zaokrąglenie.

wredulus_pospolitus: ja pierdole ... trójkąt NIE MA zaokrąglenia

wredulus_pospolitus: Ale słuszna uwaga −−− wysokość tych małych trójkątów będzie mniejsza niż h=2

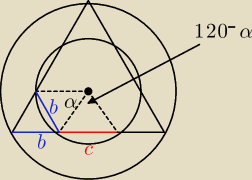
wredulus_pospolitus: 1) bok dużego trójkąta: a = 8√3 2) wprowadzamy oznaczenia: b −−−− bok małego trójkąta 3) c = a − 2b 4) z Tw. cosinusów: c² = 6² + 6² − 2*6²*cos(120−α) b² = 6² + 6² − 2*6²*cosα c = 8√3 − 2b trzy równania ... trzy niewiadome ... jedziesz

lew17: Wiec jak to wykonac?

lew17: A co to jest to c?

lew17: Czemu wziąłeś kąt 120 stopni?

wredulus_pospolitus:

wredulus_pospolitus: zrób rysunek ... zaznacz sobie ten sześciokąt ... połącz środek okręgów z każdym z wierzchołków ... zauważ, że masz trzy trójkąty z podstawą 'b' i trzy trójkąty z podstawą 'c' ... związku z

	1
tym te dwa (tutaj zaprezentowane) trójkąty mają w sumie kąt o mierze równej		pełnego
	3

	360o
kąta czyli		= 120o ... stąd to 120o
	3

lew17: ok chyba rozumiem

lew17: Ok ale nie umiem tego układ rozwiązać 4b² − 32√3 b + 192 = 72 − 72cos(120 − α) b² = 72 − 72 cos(α)

lew17: Nie wiem co zrobić z tym cosinusem 8√3b = b² + 18cos(120 − α) + 30 72cos(α) + b² = 72

wredulus_pospolitus: ojjj ... można o wiele łatwiej: 0) wyznaczasz a czyli bok dużego trójkąta 1) Wyznaczasz H_{dużego trójkąta}

	1
2) Zauważasz, że h'dolnego trójkąta z podstawą c' to nic innego jak		H
	3

	c
3) stąd		= ... z tw. Pitagorasa
	2

	c		a
4) b +		=		... stąd b =
	2		2

a dalej liczysz pola trójkątów równobocznych Jeszcze warto gdzieś wykazać, dlaczego wiemy że te małe trójkącimi o boku 'b' wiemy, ze są równoboczne

wredulus_pospolitus: PS. krok 0 nie jest jest potrzebny do kroku 1 ... ale do kroku 4 jest już niezbędny

lew17: a jak wykonać 2)?

lew17: sorry 3) jak z twierdzenia Pitagorasa?

wredulus_pospolitus: 6² = h² + (c/2)² <−−− tak

lew17: Dzieki