Trójkąt równoboczny Michałek : dzien dobry. Czy ktoś by mi pomógł z zadaniem 7? |AB| wychodzi 3. https://zapodaj.net/8c9cb97ebb5d5.jpg.html

chichi: ale pytają o współrzędne 3 wierzchołka, a nie jakąś |AB|, czym jest w ogóle A, a czym B?

Michałek : Długość odcinka podanego

Michałek : Długość boku 3

chichi: niech: A = (1,3) oraz B = (4,−1), prosta przechodząca przez te punkty

	4		13
k: y = −		x +		, prosta do niej prostopadła i przechodząca przez środek odcinka AB
	3		3

	3		7
l: y =		x −		, na tej prostej leży brakujący wierzchołek, zatem można go zapisać
	4		8

	3		7		5√3
tak: C = (c,		c −		), jeżeli |AB| = 5, to d(C,k) =		, zatem mamy
	4		8		2

	5√3		9   21   |4c + c − − 13|   4   8		5
równanie:		=		⇔ c =		± 2√3
	2		√16 + 9		2

pozostało Ci wyznaczyć rzędne dla tych punktów i masz współrzędne brakującego wierzchołka

misio: 2 sposób |AB|=5 rozwiązać układ równań (x−1)²+(y−3)²=25 i (x−4)²+(y+1)²=25

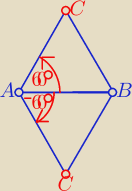misio: 3 sposób Skorzystać z równania obrotu punktu B wokół punktu A raz o kąt α= 60^o i następnie o kąt α= −60^o równania obrotu : x_C= (x_a−x_B)*cosα −(y_A−y_B)*sinα+x_B y_C= (x_a−x_B)*sinα+(y_A−y_B)*cosα+y_B i teraz tylko podstawić dane ...............