Konstrukcja
Klaudi3:
Dane są odcinki których długości są równe aib (a>b). Skonstruuj odcinek, którego długość będzie
równa:
3(a+b)/7
13 wrz 00:53
chichi:
| | 3 | |
no wystarczy odmierzyć konstrukcyjnie |
| (a + b), nie potrafisz tego zrobić? |
| | 7 | |
13 wrz 01:48
Mariusz:
Ale ta odpowiedź dużo wnosi do tematu
13 wrz 13:41
I'm back:
Mariusz... w sumie to trochę więcej niż twoja
Klaudia − czy chodzi Ci o faktyczne skonstruowanie takiego odcinka wykorzystując podstawowe
przedmioty takie jak ekierka, cyrkiel, linijka?
13 wrz 15:59
Mila:
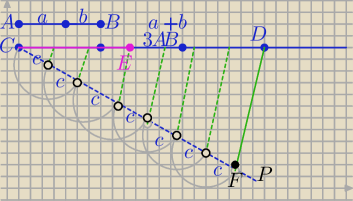
Szkic:
Trudno tu wykonać dokładną konstrukcję .
1) suma a+b=AB
2) potrojony odcinek AB
3AB=CD=3(a+b)
3) Rysujesz półprostą CP, na niej "odkładasz" 7 równych odcinków (c)
Łączysz punkty F i D
konstrukcja odcinków równoległych do FD jak pokazano na szkicu
4)
13 wrz 20:24
chichi:
nie jest to poprawnie zrobione, nie trzeba potrajać wcale |AB| = a + b
| | 3 | | 9 | |
u Ciebie wyszło |CE| > |AB| zatem |
| (a + b) > a + b, czy aby nie |CE| = |
| (a + b)?  |
| | 7 | | 7 | |
13 wrz 20:41
chichi:
(1) rysujemy dowolną prostą taką aby można było odłożyć na niej odcinek o dłg. równej a + b
(2) z dowolnego końca odcinka pod kątem ostrym do niego rysujemy półprostą
(3) odkładamy 7 krotnie ustaloną długość 'c' na tej półprostej i znacząc w tych miejscach
punkty C
1, C
2, C
3, ..., C
7
(4) łączymy C
7 z wierzchołkiem z którego nie wychodzi owa półprosta
(5) rysujemy prostą równoległą do boku z pkt. (4) przechodzącą przez C
3
(6) odl. między punktem z którego wychodzi półprosta, a punktem przecięcie prostej z pkt. (5)
| | 3 | |
to |
| (a + b) |
| | 7 | |
13 wrz 20:49
chichi:
w (6) nie dopisałem... a punktem przeciecia prostej z pkt. (5) z naszym odcinkiem oczywiście
13 wrz 20:50
Mariusz:
Tutaj należałoby wykorzystać twierdzenie Talesa
13 wrz 22:00
chichi:
ojj ja po przeczytaniu odpowiedzi Mili miałem w głowie te 7 razy, oczywiście należy odłożyć 10
razy
13 wrz 22:01
odcinek:
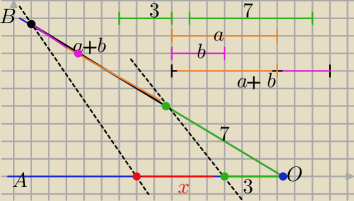
| 3 | | x | | 3(a+b) | |
| = |
| ⇒ x= |
| |
| 7 | | a+b | | 7 | |
13 wrz 22:02
Mila:
Ale wtopa. Masz rację chichi. Dziękuję za uwagę. Punkt E w innym miejscu.
Jednak , można poprawić punkt E i będzie dobrze.
Lepiej jednak z tw. Talesa.
13 wrz 23:42
chichi:
ojj, zdarza się każdemu. dużo zdrówka kochana
14 wrz 00:28
Mila:
Dzięki
Pozdrawiam.
14 wrz 01:47
an: Czy to ca pokazał @ odcinek nie jest twierdzeniem Talesa ,
a co najmniej bezpośrednio z niego nie wynika
14 wrz 02:05
Mariusz:
Jakie proporcje odcinków wynikają tutaj z podobieństwa trójkątów a jakie z twierdzenia Talesa
na rysunku @odcinka
(mamy podobieństwo trójkątów gdzie widoczna jest cecha kąt kąt kąt
oraz mamy ramiona kąta przecięte dwiema równoległymi −
czyli zachodzi także twierdzenie Talesa)
14 wrz 06:49