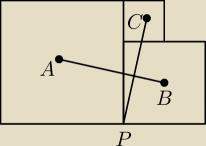
kwadraty Fuan: Na rysunku kwadraty mają środki A, B i C. Punkt P jest wierzchołkiem kwadratów o środkach A i B. Udowodnij, że PC i AB są prostopadłymi odcinkami o tej samej długości.

kerajs: Dorysuj równoległe do boków kwadratów odcinki aby powstały trójkąty prostokątne ABD i CPQ (kąty proste są w D i Q). Niech boki większych kwadratów mają długości a i b. Stąd;

	a		b
|BD|=		+
	2		2

	a		b
|AD|=		−
	2		2

	a−b
|PQ|=b+		=|BD|
	2

	a−b
|CQ|=		=|AD|
	2

Konkluzja: Trójkąty prostokątne ABD i CPQ są przystające i obrócone względem siebie o 90^o, a stąd prostopadłość odcinków |PC| i |AB|