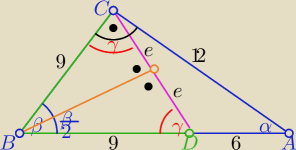
proszę o rozwiązanie anna: w trójkącie w prostokątnym ABC przyprostokątne AC i BC mają długości odpowiednio 12 i 9 Na boku AB wybrano taki punkt D że odcinki BC i BD są równe Oblicz cosinus kąta BCD , promień okręgu wpisanego w trójkąt BCD i promień okręgu opisanego na tym trójkącie obliczyłam bok AB = 15 dalej nie wiem

Mietek z fabryki żyletek: poprowadź wysokość z wierzchołka kąta prostego i dalej dość łatwo

Eta: cosγ=sin(β/2)

	9		3
cosβ=		=
	15		5

	√5
cosβ= 1−2sin2(β/2) ⇒ ......... sin(β/2)=		= cos γ
	5

	9√5
to e=9*sin(β/2) =		to 2e= ...........
	5

z tw. sinusów w ΔBDC

	2e		9√5
2R=		=................=
	sinβ		4

	2PΔDBC
r=		=.........
	9+9+2e

dokończ

Bolek z fabryki rolek:

anna: dziękuję bardzo

anna: cosβ = 1 − 2sin²(β/2) z jakiego wzoru to zostało obliczone

Eta: cos(2α)=cos²α−sin²α= 2cos²α−1= 1−2sin²α =============== ========= cosβ= 1−2sin²(β/2)

anna: dziękuję