okrąg analityczna: Napisz równanie okręgu przechodzącego przez punkty M=(−5,−12) i N=(7,4) wiedząc,ż jego środek należy do prostej p: y=x−5

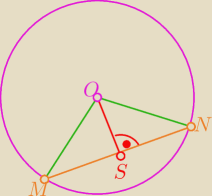
chichi: O = (s, s − 5), S = (1, −4), N = (7, 4) vec(SO) ∘ vec(SN) = 0 ⇔ [s − 1, s − 1] ∘ [6, 8] = 0 ⇔ 6(s − 1) + 8(s − 1) = 0 ⇔ s = 1 ⇒ O = (1, −4) = S jak się okazuje M i N to punkty które wyznaczają średnicę okręgu

chichi: |MN| = √(−12)² + (−16)² = √400 = 20 = 2r ⇒ r = 10 równanie okręgu o środku w punkcie O: (x − 1)² + (y + 4)² = 100