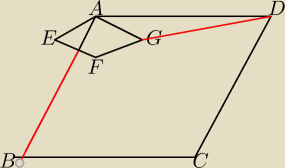
Wykaż, że zaznaczone odcinki są równej długości. jadziama: Czworokąty ABCD i AEFG na rysunku obok są rombami, w których kąty ostre mają miarę 50°. Wykaż, że |BE| = |DG|. PS. Przepraszam za taki koślawy rysunek, pierwszy raz korzystam z tej opcji.

jadziama: Na rysunku zanaczyłam na czerwono omyłkowo zły odcinek

kerajs: Skoro ∡DAG =∡BAE=25^o to trójkąty ADG i ABE są przystające, więc |BE| = |DG|.

jadziama: Chwila, ale dlaczego te kąty mają 25 stopni? Sorry, jeśli to coś oczywistego, ale nie ogarniam.

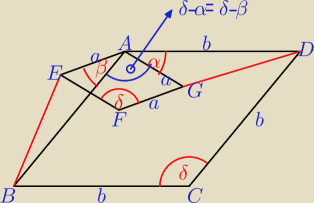
rombek: α = β Trójkąty ADG i ABE: |AD| = |AB| = b, |AG| = |AE| = a, |∡DAG| = |∡EAB| = α spełniona jest cecha przystawania trójkątów: bok − kąt − bok, zatem |DG| = |BE|

kerajs: Fakt, nie musi być to 25^o (czyli połowa kąta ostrego rombu). ∡DAG +∡GAE= ∡DAB +∡BAE Ponieważ romby są podobne to ∡DAB =∡GAE więc ∡DAG =∡BAE. Oznacza to, że trójkąty ADG i ABE są przystające, co wymusza równość: |BE| = |DG|.

jadziama: Bardzo dziękuję za pomoc