trojkat
ani123: trojkat o wymiarach 7 na 13 na 15 jak obliczyc katy zawarte w trojakcie?
1 wrz 21:07
chichi:
dróg jest wiele, możesz np. skorzystać z tw. Carnota i wyznaczyć miarę jednego z kątów, do
kolejnych dobrać się np. z tw. Sinusów, bądź też wzoru na pole, jak Ci wygodniej. jeśli dane
są dobrane "ciulowo" to znajdziesz jedynie przybliżone miary tych kątów
1 wrz 21:49
wredulus_pospolitus:
można też skorzystać z tw. cosinusów
1 wrz 22:56
ani nic:
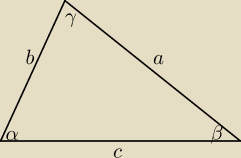
Wzory Carnota (twierdzenie cosinusów)
| | b2 + c2 − a2 | |
coa(α) = |
| |
| | 2bc | |
| | a2 + c2 − b2 | |
coa(β) = |
| |
| | 2ac | |
| | a2 + b2 − c2 | |
coa(γ) = |
| |
| | 2ab | |
Poza zadaniem. Pojawiają się objawy pandemii i zdalnych lekcji.
1 wrz 23:02
ani123: Mimo to że nie jest to trójkąt prostokątny to mogę używać funkcji trygonometrycznych?
2 wrz 06:30
2 wrz 06:39
Min. Edukacji: wg. mnie pojawia sie objaw braku samodzielności, umiejętności szukania i dociekania prawdy
2 wrz 06:40
wiceminister:
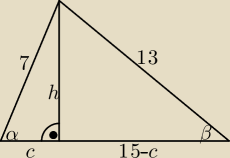
no to z trójkątami prostokątnymi
h
2 + c
2 = 49 i h
2 + 225 − 30c + c
2 = 169 ⇒ 49 + 225 − 169 = 30c ⇒ c = 3,5
| | h | | 3,5 | |
cos(α) = |
| = |
| = 0,5 ⇒ α = ... |
| | 7 | | 7 | |
| | 15 − c | | 11,5 | | 23 | |
cos(β) = |
| = |
| = |
| ⇒ β = ... |
| | 13 | | 13 | | 26 | |
γ = ...
2 wrz 20:58
prawie minister:
2 wrz 21:36
kerajs:
Z porównania pól:
| | 1 | | 1 | |
|
| ab sin (∡{a,b})= |
| √(a+b+c)(a+b−c)(a−b+c)(−a+b+c) |
| | 2 | | 4 | |
| | √(a+b+c)(a+b−c)(a−b+c)(−a+b+c) | |
sin (∡{a,b})= |
| |
| | 2ab | |
3 wrz 06:19
dyrektor departamentu:
jeszcze jedna propozycja
| | abc | |
P − pole trójkąta, R − długość promienia okręgu opisanego, R = |
| |
| | 4P | |
Biorąc od
wiceministra h =
√49 − c2 =
√49 − 12,25 = 3,5
√3, P=0,5*15*3,5
√3
| | 13 | | 7 | | 15 | |
Z twierdzenia sinusów: sin(α) = |
| , sin(β) = |
| , sin(γ) = |
| |
| | 2R | | 2R | | 2R | |
3 wrz 11:08