pytanie ~milek: Mam prośbę w zadaniu mam kulę wpisaną w ostrosłup i oblicz pole, objętość, wiem że powiniene wyjść z tego że ten ostrosłup można podzielić na ostrosłupy których wysokością będzie promień tej kuli i one będą mieć wspólny wierzchołek w środku tej kuli, a ściany tego ostrosłupa to ich podstawy, dobrze myślę ? Czy tak będzie z każdą kulą w dowolnym ostrosłupie ? Nie wiem czy rozumiecie, bo widzę to, ale nie potrafię narysować, zwłaszcza tutaj

chichi: wrzuć zdjęcie na zapodaj

~milek: mam rozwiązanie, mi chodzi tylko o to czy każdy ostrosłup z wpisana w środku kula można uznać ze składa się z 4 ostrosłupów, których podstawami są ściany boczne tego głównego ostrosłupa,a ich wysokością będzie promień kuli, mi to wyszło, ale nie wiem czy tak jest z każdym ostrosłupem opisanym na kuli?

Mila: Tak

chichi: nawet gdy w podstawie jest dowolny n−kąt?

kerajs: To ogólna własność brył w które można wpisać kulę. Można je podzielić na ostrosłupy o podstawach będących ścianami bryły i wysokościach równych promieniowi kuli wpisanej,

	Pr
Stąd i wzór na objętość takich brył: V=		; gdzie P to pole bryły, a r to promień kuli.
	3

chichi: P to pole bryły?

~milek: Dzięki o to mi właśnie chodziło, ale nie umiem tego tu narysowac, zreszta u siebie tez mam to słabo

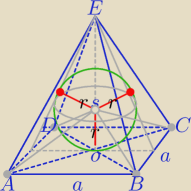
Mila: Przykład. Kula wpisana w ostrosłup prawidłowy czworokątny:

	1		1
VABCDE=		(P□ABCD*r+4*PΔBCE*r}=		Pc*r
	3		3

Analogicznie dla innych ostrosłupów opisanych na kuli.

kerajs: ''chichi: P to pole bryły?'' Tak. Napisałem to także w ostatnim zdaniu odpowiedzi z 6:16 .

Mila: Miało być pole powierzchni całkowitej ostrosłupa. Chyba o to chodzi chichi ?