Nierówność trygonometryczna Karsi: Rozwiąż nierówność w przedziale [−π,π] (Sin2x−¹₂)(Cos2x−^√2₂)≤0

chichi: i problem polega na?

Karsi: Nie wiem jak wyznaczyć przedziały z rysunku bo mamy cosinus i sinus

Min. Edukacji:

	√2
Sin2x≤1/2 lub cos2x≤
	2

Karsi: Czyli iloczyn tych wyrażeń będzie niedodatni gdy kazde to wyrażenie będzie niedodatnie?

wredulus_pospolitus: heee (−1)*(−1) daje Ci liczbę niedodatnią

wredulus_pospolitus: dokładnie jeden z nawiasów ma przyjmować ujemną wartość (bądź którykolwiek z nich ma dawać wartość równą 0)

Karsi: Właśnie nie daje, rozpatrywałem ta zależność łącznie, ale widzę, ze można oddzielnie. Ok

wredulus_pospolitus: a*b ≤ 0 ⇔ ( a < 0 ∧ b > 0 ) ∨ ( a > 0 ∧ b < 0 ) ∨ ( a = 0 ∨ b = 0 )

Min. Edukacji:

7π

7π

π

π

π

5π

7π

<−

;−

>∪<−

;

>∪<

;

>∪<

;π>

8

12

8

12

8

12

8

o ile sie nie powie.. w rachunkach

Karsi: Czyli wystarczy rozpatrzyć warunek min. Edukacji?

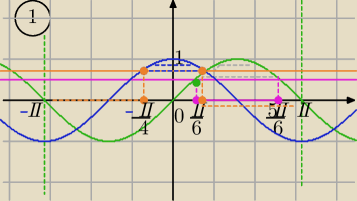
Mila: Na rysunku: y=sin(x), y=cos(x) 1)

	1		√2
sin(2x)≥		i cos(2x)≤
	2		2

	π		5π		π		π
		+2kπ≤2x≤		+2kπ i [ −π+2kπ≤2x≤−		+2kπ lub		+2kπ≤2x≤π+2kπ ]
	6		6		4		4

część wspólna :

π		5π
	+2kπ≤2x≤		+2kπ /:2 i x∊<−π,π>
4		6

π		5π
	+kπ≤x≤		+kπ
8		12

	π		5π
k=0 to		≤x≤
	8		12

	7π		7π
k=−1 to −		≤x≤−
	8		12

lub Narysuj sobie drugi rysunek , tylko inne przedziały będą pasowały do nierówności:

	1		√2
sin(2x)≤		i cos(2x)≥
	2		2

dla cosinusa :

−π		π		π
	+2kπ≤2x≤		+2kπ i dla sinusa −π+2kπ≤2x≤		+2kπ
4		4		6

część wspólna

−π		π
	+2kπ≤2x≤		+2kπ/:2
4		6

−π		π
	+kπ≤x≤		+kπ
8		12

k=0

−π		π
	≤x≤
8		12

k=1

−π		π		7π
	+π≤x≤		+π⇔		≤x≤π ( reszta wykracza poza pi)
8		12		8

k=−1

	11π
−π≤x≤−
	12

wredulus_pospolitus: warunek z 12:17 jest NIEPOPRAWNY (umożliwia sytuację gdy oba nawiasy są niedodatnie, a to nie wchodzi w skład prawidłowego rozwiązania) warunek z 10:47 jest poprawny

chichi: jeszcze parę dni i forum odżyje

Min. Edukacji: Tak , zacznie sie odrabiania prac domowych hurtem😁

Min. Edukacji: @Karsi masz rozpatrzyc kiedy iloczyn dwóch wyrażeń jest mniejszy bądź równy zeru , czyli (Sin2x ≤0,5 ∧ cos2x≥0,7) ∨ (sin2x≥0,5 ∧ cos2x ≤0,7) to co Ci napisałem wczesniej to był początek, polowa tego co masz zrobić Mila to ładnie rozrysowala, pytanie czy rozumiesz o co w tym chodzi🤔

Karsi: Jak najbardziej czaje o co chodzi, tylko pogubiłem się w tym całym zamieszaniu. Pozdrawiam

kerajs: Wydaje się mi, że są prostsze sposoby rozwiązywania nierówności typu: wyrażenie większe/ mniejsze/ niewiększe/ niemniejsze od zera. Przykładowo: Rozwiązuje się równanie, na osi zaznacza pierwiastki oraz wskazuje ich parzystne wielokrotności. Istnieją dwie możliwości przeprowadzenia ''fali znaku wyrażenia'', więc wybiera się dowolny punkt który nie jest pierwiastkiem i określa znak wartości wyrażenia dla wybranego argumentu, a on wskazuje właściwą ''falę znaku''. Pozostaje z rysunku odczytać rozwiązanie nierówności.

daras: nikt tego tak już nie uczy

kerajs: A może wiesz dlaczego ''nikt tego tak już nie uczy''?

daras: nie wiem, przygodę ze szkołą skończyłem wieki temu