największe pole maturalny: Obwód trójkata prostokątnego jest równy 2 Jakie największe pole ma taki trójkąt?

chichi: bez większego zastanowienia, niech przyprostokątne będą długości a,b > 0, a przeciwprostokątna długości c, z polecenia mamy, że: a + b + c = 2 ⇒ c = 2 − a − b z tw. Pitagorasa mamy: a² + b² = (2 − a − b)² ⇒ a² + b² = 4 + a² + b² − 4a − 4b + 2ab ⇒

	2(b − 1)
⇒ a =
	b − 2

	1		2(b − 1)
S(b) =		b		, wyznacz dziedzine tej funkcji i znajdź jej ekstrema
	2		b − 2

as: a,b,c >0 a+b+c=2 , 2S_Δ=ab , c=√a²+b² <2 z nierówności między średnimi a+b≥2√ab= 2√2S a²+b²≥2ab=4S √a²+b²≥2√S , równość zachodzi dla a=b 2=a+b+c ≥2√2S+2√S / : 2 1 ≥√2S+√S

	1
√S≤
	√2+1

	1
S≤
	(√2+1)2

	1
Smax=		= 3−2√2
	(√2+1)2

======================

chichi: super rozwiązanie, dlatego w swoim wpisie zaznaczyłem, że bez większego zastanowienia, bo było ono najbardziej łopatologiczne, dla mało ambitnych maturzystów

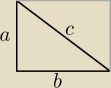
Mila: Spośród prostokątów o stałym obwodzie największe pole ma kwadrat. W takim razie trójkąt prostokątny o stałym obwodzie , który ma największe pole jest połową kwadratu. ⇔a=b c=a√2 a+a+a√2=2 2a +a√2=2 a(2+√2)=2 /*(2−√2 2a=2(2−√2) a=2−√2

	1
PmaxΔ=		(2−√2)2=3−2√2
	2

maturalny: Najpierw trzeba to wykazać ? tak myślę

Mila: Tak, możesz wykazać to co dotyczy prostokątów. Nie będziesz mieć przy tym problemu.