nierówność anonim123:

	1−x
jak rozwiązać nierówność 1−√2<		?
	x

: x≠0 (1−√2)x²<(1−x)x x((1−√2)x−(1−x))<0 x((2−√2)x−1)<0

	1
x∊(0 ;		)
	2−√2

anonim123: A skąd jest ostatnia nierówność?

antoni: Jak Ty się z taką wiedzą ( dokładnie z jej brakiem ) dostałaś na te studia ?

kerajs: x((1−√2)x−(1−x))<0 x((1−√2)x−1+x)<0 x(((1−√2)+1)x−1)<0 x((1−√2+1)x−1)<0 x((2−√2)x−1)<0

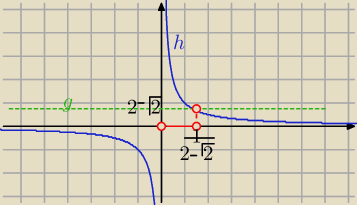
ak: graficznie x≠0

1−x
	>1−√2
x

	1
		>2−√2
	x

	1
h(x)=		, h(x)= 2−√2
	x

h(x) >g(x)

	1
x∊(0,
	2−√2)

===========

chichi: punkt przecięcia I tak trzeba by namierzyć algebraicznie, więc graficznie raczej trudno w tym przypadku według mnie, ale wykres zawsze fajnie zobaczyć, że wszystko się zgadza

ak:

1		1
	=2−√2 ⇒ x=		i co tu trudnego ?
x		2−√2

ak: Ważnniejsze, by "anonim.." nie został nauczycielem

chichi: ja nie mówię, że trudno, tylko gdy mowa o graficznym rozwiązaniu, to zazwyczaj najlepiej to działa, gdy wykresy przecinają się w punktach kratowych, to rozwiązanie bardziej nazwałbym algebraiczno−graficznym, ale wyznaczenie tego punktu jest banalne więc twoje rozwiązanie jest równie szybkie