sześciany visualtix: dany jest szescian o krawedzi 1 cm a) wybieramy losowo 2 wierzcholki szescianu. zmienna losowa przyporzadkowywuje wybranym dwóm punktom odleglosc miedzy nimi. oblicz wartosc oczekiwana tej zmiennej B) wybieramy losowo 3 wierzcholki szescianu. zmienna losowa przyporzadkowywuje wybranym trzem punktom pole trojkata, ktorego sa wierzcholkami. oblicz wartosc oczekiwana tej zmiennej

kerajs:

	12		12		4
E(a)=1*		+√2*		+√3*
	28		28		28

	1		24		√2		24		3√3		4
E(b)=		*		+		*		+		*
	2		56		2		56		4		56

ite: Czy w podpunkcie A) polecenie 'wybieramy losowo 2 wierzchołki sześcianu' można też rozumieć jako wybór dwóch niekoniecznie różnych wierzchołków?

kerajs: Przyjąłem, iż ''wybieramy losowo 2 wierzcholki szescianu.'' oznacza jeden wybór dwóch (więc różnych) wierzchołków. Jednak przyznaję, że można ten wybór doprecyzować, aby był bardziej jednoznaczny.

uczen: a jest ktoś w stanie wytłumaczyć te działania 12/28 i te iloczyny bo nie bardzo wiem co sie skąd bierze tuta j

ite: Żeby nie mieć wrażenia, że wartość oczekiwana zmiennej losowej pojawia się znikąd: − zacznij od określenia wartości tej zmiennej (czyli możliwych odległości między wierzchołkami sześcianu o boku 1 cm), − ustal prawdopodobieństwo wylosowania wierzchołków odległych o każdą z tych wartości, − zapisz rozkład zmiennej losowej, − podstaw wartości występujące w rozkładzie do wzoru EX = ... będziesz dokładnie wiedzieć, co po kolei kerajs napisał 08:34

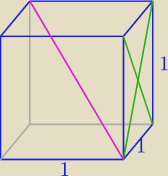
Mila: 8− liczba wierzchołków 2 wierzchołki możemy wylosować na :

8 2		8*7
	=		=28 sposobów
		2

Wśród 28 odcinków mamy odpowiednio : 1) 12 odcinków o długości 1 ( krawędzie sześcianu) 2) 6*2=12 odcinków o długości √2 ( przekątne ścian) 3) 4 odcinki o długości √3 ( przekątne sześcianu) X− zmienna losowa X | 1 √2 √3 ================

	12		12		4
p1 |
	28		28		28

−−−−−−−−−−−−−−−−−−− E(X)=x₁*p₁+x₂*p₂+x₃*p₃ x_i− wartości zmiennej losowej, p_i− prawd.

	12		12		4
E(X)=1 *		+ √2*		+ √3*
	28		28		28

	3+3√2+√3
E(X)=
	7

=================

uczen : a rozumiem ale mam chyba jakies przycmienie umyslu i nie jestem w stanie dociec skad te liczby w b) bo wiem ze przypadkow jest 56 ale czemu nagle z 12 zrobilo sie 24 skoro to ta sama figura?

uczen : bo wydaje mi sie ze w obrebie jednej sciany mozna wybrac 3 wierzcholki na 4 sposoby wiec 24/56 i pole takiego trojkata to 1*1*0.5 = 0.5 ale do tych kolejnych nie jestem w stanie dojść

Mila: Jutro wyjaśnię.

Uczen: dziękuję

kerajs: Pozostałe to: 24 trójkąty prostokątne bokach 1,√2, √3 4 trójkąty równoboczne o boku √3

uczen : ale jakim cudem może powstać trójkąt o równych wszystkich bokach długości √3 skoro tyle wynosi przekątna sześcianu ja widze tylko takie o bokach √2 który towrzą Trójkąt równoboczny wspólnie przekątne ścian bocznych i podstaw sześcianu.

uczen : i w odpowiedach jest odpowiedz w b) inna niż wychodzi ta co napisał kerajs w odp jest 1/14(3 + 3√2 +√3)

Mila:

	8 3		1
Liczba Δ:		=		*8*7*6=56
			6

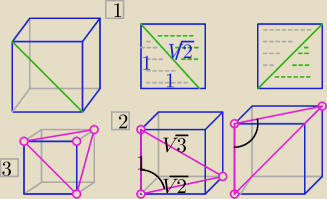
1) na każdej ścianie 4 Δ o bokach :1,1 ,√2

	1
PΔ=
	2

	1
Razem: 6*4= 24 Δ o polu :
	2

2) Od każdej krawędzi dwa Δ o bokach: 1,√2,√3

	1		√2
PΔ=		*1*√2=
	2		2

	√2
Razem: 12*2=24 Δ o polu:
	2

3) 8 Δ równobocznych o boku: √2

	√3
PΔ=
	2

==================== 4)

	1		24		√2		24		√3		8
E(X )=		*		+		*		+		*		=
	2		56		2		56		2		56

	1		3		√2		3		√3		1
=		*		+		*		+		*		=
	2		7		2		7		2		7

	3+3√2+√3
=
	14

=================

uczen: baaaaaaaaaaardzo ci dziękuje