mat. 18 seba: W dowolnym czworokącie łączymy środki boków. Udowodnij, że: a) otrzymana figura jest równoległobokiem b) pole równoległoboku jest równe połowie pola czworokąta

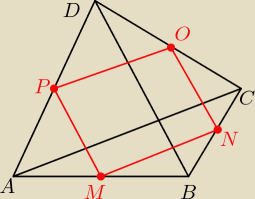
Basia: MN || AC i OP||AC ⇒ MN||OP NO||BD i MP||BD ⇒ NO||MP stąd: MNOP jest równpległobokiem △MAP ∼△BAD w skali 1:2 △MBN ∼△ABC w skali 1:2 △NCO ∼△BCD w skali 1:2 △PDO ∼△ADC w skali 1:2 stąd P_MAP=¹₄P_BAD P_MBN=¹₄P_ABC P_NCO=¹₄P_BCD P_PDO=¹₄P_ADC P_MNOP=P_ABCD−P_MAP−P_MBN−P_NCO−P_PDO= P_ABCD−¹₄*[ P_BAD+P_ABC+P_BCD+P_ADC] = P_ABCD−¹₄*[ (P_BAD+P_BCD)+(P_ABC+P_ADC)] = P_ABCD−¹₄*[ P_ABCD+P_ABCD] = P_ABCD−¹₄*2*P_ABCD = P_ABCD−^{1}2}P_ABCD=u{1}₂P_ABCD

Basia: ostatnia linia: =P_ABCD−¹₂P_ABCD=¹₂P_ABCD

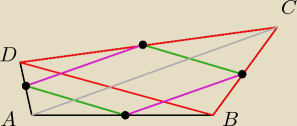
Godzio: Jest takie twierdzenie: Odcinek łączący środki 2 boków trójkąta jest równoległy do 3 boku i równa się połowie jego długości, korzystając z tego wiemy że te 2 zielone odcinki są równoległe do przekątnej BD a zarazem podstawy trójkąta ABD i BCD więc są one równoległe, na tej samej zasadzie te 2 fioletowe odcinki więc otrzymana figura jest równoległobokiem z b spróbuj sam

Basia: "takie twierdzenie" wynika z podobieństwa trójkątów tr. AMN ~ tr.ABD na mocy cechy bkb ⇒ ∡M=∡B i ∡N=∡D ⇒ MN||BD i |MN|=¹₂|BD| albo jak kto woli z tw.odwrotnego do tw.Talesa