trójkat Magnificent: Niech ABC będzie trójkątem prostokątnym o kącie w A równym 90 stopni i BC=10. Niech P będzie takim punktem na AB, że BP=2. Niech Q będzie takim punktem na AC, że CQ = 4. Jeśli prosta PQ przechodzi przez środek okręgu wpisanego w trójkąt ABC , znajdź możliwe wartości pola APQ https://foto-hosting.pl/img/9d/4b/b6/9d4bb636be5af0d2eaced50c43ed3271b1e19425.jpeg

Ferdynand:

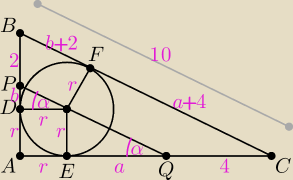
	b		r
podpowiedź do jednej z dróg: b = 4 − a,		=
	r		a

|AB| = r + b + 2 = r + 4 − a + 2 = r − a + 6, |AC| = r + a + 4, |AB|² + |AC|² = 100

	1		1
Pole trójkąta APQ: PAPQ = r2 +		br +		ar = ...
	2		2

Magnificent: Ok wyszło pole r=2,b=2,a=2 P=8 a w odpowiedzi jest 8 oraz 1200/169. Jak dojść do tej drugiej odpowiedzi?

Ferdynand:

	24
W trakcie rozwiązywania otrzymujemy równanie: 13r2−50r+48=0, stąd r = 2 lub r =
	13

Szukane pole P_APQ = r² + 2r

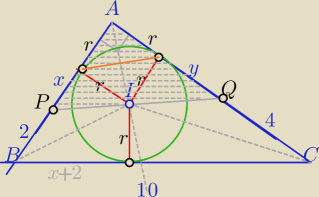
Mila: 1) W ΔABC: r+x+2+r+y+4=2r+2R⇔ x+y+6=10 x+y=4 2)

	1		1		1
PPAQ=r2+		x*r+		y*r=r2+		r*(x+y)=r2+2r
	2		2		2

3) xy=r² z podobieństwa Δ ( jak u Fer.) albo porównanie pól. y=4−x x*(4−x)=r² x²−4x+r²=0 x=2−√4−r² lub x=2+√4−r² i r∊(0,2)⇔ x=2−√4−r² i y=4−2+√4−r²=2+√4−r² 4) p=r+10− połowa obwodu ΔABC

1
	|AB|*|AC|=p*r − porównanie pól
2

(r+4−√(4−r²))*(r+6+√(4−r²))=2r(r+10) stąd : 10−5r=√4−r² i równanie jak u Fer. 13r²−50r+48=0 Nie wiem czy to łatwiejszy rachunek, ale z tw. Pitagorasa zniechęciły mnie kwadraty wyrażeń. Może jeszcze coś łatwiejszego znajdzie się.

Kiepski: