mat. 16
seba: W okrąg o promieniu r wpisano kwadrat i na tym samym okręgu opisano trójkąt równoboczny. Oblicz
długość promienia okręgu wiedząc, że suma długości boku kwadratu i boku trójkąta równobocznego
jest równa 12.
6 mar 22:47
Godzio:
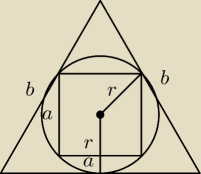
d = a
√2
a + b = 12
a = 12−b
b
√3 = 3(12−b)
√2
b
√3 = 36
√2 −3
√2b
b
√3 + 3
√2b = 36
√2
b(
√3+3
√2) = 36
√2
| | 36√2(√3−3√2) | | 36√6 − 216 | |
b = |
| = |
| |
| | 3−18 | | −15 | |
| | b√3 | | 36√6 − 216 | | 1 | | 6√6−36 | |
r = |
| = |
| * √3 * |
| = |
| * √3 = |
| | 6 | | −15 | | 6 | | −15 | |
| 18√2 − 36√3 | | −6√2 + 12√3 | |
| = |
| |
| −15 | | 5 | |
Taki troche dziwny wynik więc sprawdź obliczenia
6 mar 22:58
