kwadrat tryftek: Dany jest kwadrat ABCD oraz punkty P na AB i Q na BC. Punkt R∊PQ tak, że PR=2,QR=3,DR=4, kąt PRD=kąt PAD. Jaka jest powierzchnia kwadratu ABCD?

kerajs: Moim zdaniem ten kwadrat jest prostokątem o bokach 24/5 i 22/5.

kerajs: Sorry, chyba się nie obudziłem pisząc powyższy post. Przyjmując że ''PR=2,QR=3,DR=4, kąt PRD=kąt PAD'' wychodzi mi, że to kwadrat o boku 2√5, jednak wtedy P=A (!).

tryftek: czemu tak?

an: Kwadrat 20 j.k.

kerajs: Dorysuj proste równoległe do boków i przechodzące przez punkt R. Ich przecięcia z obwodem oznacz jako E (na AB), F (na BC), G (na CD) i H (na AD). Trójkąty EPR, FQR, DHR są podobne do trójkąta BPQ (w którym |BP|=y, a |BQ|=x). |AE|+|EB|=|AH|+|HD|

4		3		2		4
	x+		y=		x+		y
5		5		5		5

y=2x Z tw. Pitagorasa wyliczysz x=√5 i y=2√5

	4		3
Niestety		x+		y=y co sprawia że P=A, więc nie istnieje kąt PAD (lub w innej
	5		5

interpretacji jest on dowolny). Konkluzja: kwadrat sugerowany w treści zadania nie istnieje.

tryftek: Czemu tak

tryftek: To już nie wiem bo an bo podaje ze 20

kerajs: Podaje tak, gdyż (2√5)²=20. Jednak dla uzyskania tego wyniku przyjęto, że kąt PAD (więc i kąt PRD) jest prosty, lecz z zadania wychodzi że ramię |AP|=0. Jaki więc jest naprawdę kąt PAD?

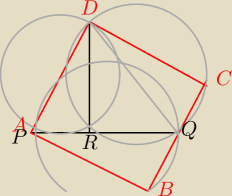
an: Z tym kątem jest problem jednak on "ślizgając się po okręgu zbliża się do 90^o"

kerajs: Tu jest narzucony układ statyczny, więc o jakim ''ślizganiu się'' piszesz? PS Jeśli w treści zadania zmniejszyć odcinek DR na dowolny z przedziału (3,4) to uzyska się pewien kwadrat, lecz wtedy punkt P nie będzie należał do odcinka AB. Czy wtedy odpowiedzią powinno być pole uzyskanego kwadratu, czy stwierdzenie że kwadrat z zadania nie istnieje?

an: Ja mówię o przybliżeniu "prawie doskonałym", ale fakt, że matematycznie nie spełnia warunków zadania.