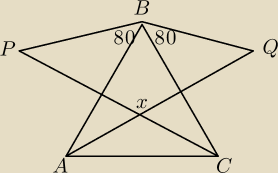
trójkąt równoramienny olaf: Wiemy ze AB=PB i BQ=BC. Oblicz kąt x.

ite: Trójkąt ABC jest dowolnym trójkątem?

olaf: równoramienny

olaf: jednak w tresci nie ma ze równoramienny

olaf: geogebra pokazuje ze 100, ale jak to zrobic? https://zapodaj.net/images/b4b8ee445a518.jpg

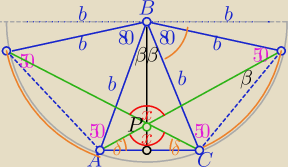
falo: ΔABC równoramienny

	1
δ=		*80o ⇒ δ=40o
	2

x= 180^o−2δ x=100^o

olaf: Skąd ABC równoramienny?

falo: Z treści zadania,bo ΔABP≡ΔCBQ

ite: Halo falo, czy z podanych o 10:20 danych nie wynika jedynie, że ΔABP∼ΔCBQ (kkk) ?

ite: jeszcze wspomagacz dla dowolnego trójkąta https://www.geogebra.org/geometry/npvnrygm

ite: poprawiam link https://www.geogebra.org/m/pjguc7ww

falo: A "młody"... nabazgrał byle jaki rysunek

falo: 13:25 racja iteracja

olaf: Tak wygląda w oryginale:https://zapodaj.net/images/8664c526768cd.jpg

falo: Na rys. AB≠PB i BC≠BQ ?

olaf: Ale w treści zadania było napisane AB=PB i BQ=BC

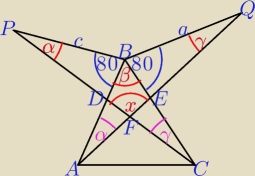
Bogdan: |AB| = |PB| = c, |BQ| = |BC| = a, |∡PBC| = |QBA| = 80^o + β, zatem ΔPBC ≡ ΔABQ ⇒ |PC| = |AQ| = b i |∡BPC| = |∡BAQ| = α i |∡BQA| = |∡BCP| = γ, w przystających trójkątach PBC i ABQ: α + β + 80^o + γ = 180^o ⇒ α + β + γ = 100^o, w czworokącie BDFE: |∡BDF| = 80^o + α, |∡BEF| = 80^o + γ, β + (80^o + α) + x + (80^o + γ) = 360^o ⇒ x + 100^o = 200^o