Wzór bayersa Ola: Czym się różni wzór bayesa od wzoru na prawdopodobieństwo całkowite Kiedy stosuje się ten a kiedy ten? Bo z definicji nie widzę różnicy A wzory sa inne .

ite: Polecam obejrzenie https://www.youtube.com/watch?v=HZGCoVF3YvM Ciepły baryton Granta Sandersona wyjaśnia najlepiej.

Ola: A po polsku

ite: https://pl.khanacademy.org/math/ap-statistics/probability-ap/stats-conditional-probability/v/bayes-theorem-visualized

potrzebujacy: obejrzałam ten film z khan ale nie widzę tu wytłumaczenia różnicy między wzorem na prawdopodobienstwo calkowite P(A) = P(B1) * P(A I B1) + P(B2) * P(A I B2) + ... od wzoru bayesa poza tym nie do konca wiem czemu w internecie uzywa sie wzoru P(AIB) =( P(B I A) * P(A) ) / P(B) a ja mam w książce w mianowniku więcej wymnożen tj. P(B1) * P(AIB1) + P(B2) * P(AIB2)

potrzebujaca ola: a dobrze to rozumiem? zadanie takie w 1 urnie sa 3 kule biale i 2 czarne a w 2 urnie 4 biale i czarna. wybieramy losowo urne i jedna kule oblicz prawdopob. ze wylosowana kula pochodzi z 1 urny jesli wiemy ze jest biala. i rozwiazujemy tym wzorem bayesa zaczynajac B1 − wylosowano pierwsza urne i A − kula jest biala B2 − 2 urna P(B1 I A) = ... i chodzi o to że wzorem bayesa możemy liczyć prawdopodobieństwo tej szczegolnej sciezki gdzie jest poszczegolna urna i poszczegolny kolor a prawdopodobienstwem calkowitym mozna by tylko policzyc jaka jest szansa na wylosowanie danego koloru bo we wzorze jest P(A) = ... i nie ma warunku czy w ogole nie o to chodzi ?

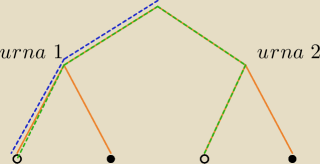
ite: tak, można to tak sobie wyobrazić jako wybranie najpierw ścieżek do kul białych, a potem tej z nich, która prowadzi do kul białych z pierwszej urny

ite: Ale, jeśli zdarzenie A polega na wylosowaniu kuli białej, to we wzorze na P(A) występują prawdopodobieństwa warunkowe, bo tu trzeba użyć wzoru na prawdopodobieństwo całkowite. A w nim występują prawd. warunkowe.

ite: Podsumowując: − wzoru na prawdopodobieństwo całkowite należy użyć, żeby obliczyć prawdopodobieństwo wylosowanie kuli określonego koloru (z którejkolwiek urny). − wzoru Bayesa użyjemy, jeśli znamy kolor wylosowanej kuli i chcemy poznać prawdopodobieństwo, że wyciągnięto ją z konkretnej urny.

potrzebujaca ola: własnie o to mi chodziło! dzięki