funkcja odwrotna wq: Pomoże mi ktoś rozwiązać problem, z którym się borykam. Mam zadanie analizy matematycznej. Mam problem tylko z pewnym fragmentem, bo za cholere nie mogę zrozumieć tego. Brzmi tak: "Niech f:R−>R, f(x)=x³+1". Wyjaśnij dlaczego istnieje funkcja odwrotna do f(x). Wiem że funkcja odwrotna to funkcja, która każdej wartości(z osobna) przyporządkowuje dokładnie jeden argument. Jak to odnieść do tego zadania. Czy w rozwiązaniu tego problemu jest tutaj istotny ten element f:R−>R. Nie jestem zbyt dobry z tej matematyki, ale chciałbym to zmienić. Cały czas nad tym pracuje ale z niektórymi rzeczami mam jeszcze problem.

wq: Pytam poważnie. Serio potrzebna mi z tym pomoc bo mam z tego egzamin we wrześniu

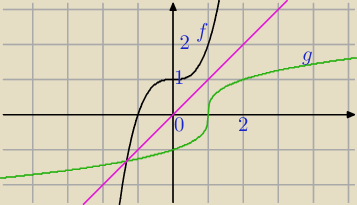
Mila: Funkcja jest odwracalna wtedy i tylko wtedy, gdy dla każdego argumentu istnieje odpowiadająca mu jedna wartość. ( funkcja różnowartościowa) Oznacza to, że każdej wartości odpowiada dokładnie jeden argument. W ten sposób, gdy odwrócimy odwzorowanie, to wynik będzie nadal funkcją. Funkcję różnowartościową nazywamy też funkcją odwracalną. Wykres funkcji f(x) i wykres funkcji odwrotnej do niej są symetryczne względem prostej y=x. Twój przykład. f(x)=x³+1 f⁻¹(x)=³√x−1 Nie mylić z odwrotnością funkcji, którą zapisujemy:

	1
[f(x)]−1=
	f(x)

Mariusz: Mila a czy to że funkcja jest różnowartościowa to tylko jeden z warunków istnienia funkcji odwrotnej ? Jeżeli dobrze pamiętam to każda bijekcja jest funkcją odwracalną