postać trygonometryczna liczby zespolonej
aga:
Cześć, jak mam zapisać postać trygonometryczna liczby zespolonej: −1−√3
skoro sin=−1/2 a cos= −√3/2
Rez= −1
Imz= −√3
|z|=2
czy kąt musze policzyć w ten sposób?:
α=arctg((−1/2)/(−√3/2))=arctg(1/√3)=π/6
8 sie 13:44
aga: mam też problem z wyznaczeniem w postaci trygonometrycznej liczby zespolonej
z=sinα + icosα
8 sie 14:12
kerajs:
| | 2π | | 2π | |
−1−√3=2(cos( |
| ) + i sin( |
| )) |
| | 3 | | 3 | |
| | π | | π | |
sinα + i cosα=cos ( |
| −α) + i sin ( |
| −α) |
| | 2 | | 2 | |
8 sie 14:22
Mila:
Zadanie 1.
Zdaje się, że zgubiłaś ' i " w zapisie liczby
z=−1−
√3 i
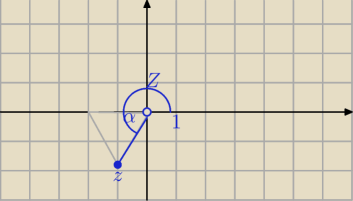
geometryczna interpretacja w tym zadaniu jest prosta.
punkt : (−1,−
√3)
|z|=
√12+(√3)2=2
widzisz, że kąt III ćwiartki
| | 4π | | 4π | |
z=2*(cos |
| +i sin |
| )− postać trygonometryczna. |
| | 3 | | 3 | |
II sposób
|z|=2
Odwrotnie zapisałaś wartości funkcji.
8 sie 17:35
kerajs:
Ech, chciałem te 240
o zapisać jako 2/3 całego łuku, ale w pośpiechu zgubiłem dwójkę.
Miało być
| | 2(2π) | | 2(2π) | |
−1−i √3=2( cos |
| +i sin |
| ) |
| | 3 | | 3 | |
Sorry.
8 sie 20:52
Mila:

8 sie 22:08
 Zadanie 1.
Zdaje się, że zgubiłaś ' i " w zapisie liczby
z=−1−√3 i
geometryczna interpretacja w tym zadaniu jest prosta.
punkt : (−1,−√3)
|z|=√12+(√3)2=2
widzisz, że kąt III ćwiartki
Zadanie 1.
Zdaje się, że zgubiłaś ' i " w zapisie liczby
z=−1−√3 i
geometryczna interpretacja w tym zadaniu jest prosta.
punkt : (−1,−√3)
|z|=√12+(√3)2=2
widzisz, że kąt III ćwiartki
