Basia:
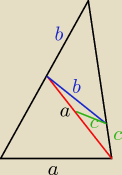
jeżeli ten proces dzielenia może być nieskończony, to mogłoby to wyglądać tak jak na rysunku
nie podejmuję się udowodnić, że da się to zrobić w skończonej liczbie kroków
Bogdan:
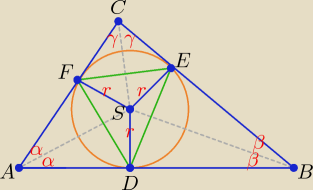
Środek okręgu wpisanego w trójkąt jest punktem przecięcia dwusiecznych kątów wewnętrznych
trójkąta.
Trójkąty ADS i AFS są przystające, więc |AD| = |AF|, trójkąt ADF jest równoramienny.
Trójkąty DBS i BES są przystające, więc |DB| = |BE|, trójkąt DBE jest równoramienny.
Trójkąty CES i CFS są przystające, więc |CE| = |CF|, trójkąt FEC jest równoramienny.
|DS| = |ES| = |FS| = r, trójkąty DES, EFS, FDS są równoramienne.
Każdy trójkąt posiada wpisany w siebie okrąg, a więc każdy trójkąt można podzielić
na trójkąty równoramienne, są to trójkąty: ADF, DBE, FEC, DES, EFS, FDS,
co należało wykazać.
