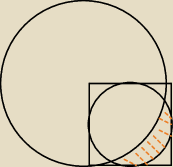
 Dany jest kwadrat o boku 4. Oblicz pole pomarańczowej częsci.
Dany jest kwadrat o boku 4. Oblicz pole pomarańczowej częsci.
| 5√2 | ||
Dorysuj trójkąt AOS. Mo on boki: 2, 2√2, 4 więc cos (ASO)= | , a cos | |
| 8 |
| −√2 | ||
(SOA)= | ||
| 4 |
| −√2 | ||
gdzie Pw0 to pole wycinka koła o środku w O i o kącie 2π−2arccos | ||
| 4 |
| 5√2 | ||
a PwS to pole wycinka koła o środku w S i o kącie 2arccos | ||
| 8 |
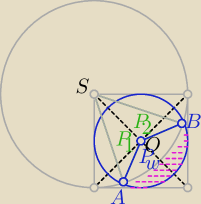 P= 2 PΔAOS +Pw(AOB) − PW(SAB)
P= 2 PΔAOS +Pw(AOB) − PW(SAB)
| 5−√7 | −5−√7 | |||
A = ( | , | ) | ||
| 2 | 2 |
| 5+√7 | −5+√7 | |||
B = ( | , | ) | ||
| 2 | 2 |
| (t2−1) | ||
x=4 | ||
| t2+1 |
| 2t(t2+1)−2t(t2−1) | ||
dx = 4 | dt | |
| (t2+1)2 |
| 2t(t2+1−t2+1) | ||
dx =4 | dt | |
| (t2+1)2 |
| 16t | ||
dx = | dt | |
| (t2+1)2 |
| t2−1 | ||
(4−x)t = (4−4 | )t | |
| t2+1 |
| t2+1−t2+1 | ||
(4−x)t =4( | )t | |
| t2+1 |
| 8t | ||
(4−x)t = | ||
| t2+1 |
| 128t2 | 128t2+128t4 | −128t4 | ||||
∫ | dt = ∫ | dt+∫ | dt | |||
| (t2+1)3 | (t2+1)3 | (1+t2)3 |
| 128t2 | 128t2 | (32t3)(−4t) | ||||
∫ | dt =∫ | dt+(∫ | )dt | |||
| (t2+1)3 | (t2+1)2 | (1+t2)3 |
| 128t2 | 128t2 | 32t3 | 96t2 | |||||
∫ | dt =∫ | dt+ | −∫ | dt | ||||
| (t2+1)3 | (t2+1)2 | (1+t2)2 | (1+t2)2 |
| 128t2 | 32t3 | 32t2 | ||||
∫ | dt = | +∫ | dt | |||
| (t2+1)3 | (1+t2)2 | (t2+1)2 |
| 128t2 | 32t3 | (−16t)(−2t) | ||||
∫ | dt = | +∫ | dt | |||
| (t2+1)3 | (1+t2)2 | (t2+1)2 |
| 128t2 | 32t3 | 16t | 1 | |||||
∫ | dt = | − | + 16∫ | dt | ||||
| (t2+1)3 | (1+t2)2 | t2+1 | 1+t2 |
| 128t2 | 32t3−16t(1+t2) | 1 | ||||
∫ | dt = | + 16∫ | dt | |||
| (t2+1)3 | (1+t2)2 | 1+t2 |
| 128t2 | 16t3−16t | |||
∫ | dt = | + 16arctg(t)+C | ||
| (t2+1)3 | (1+t2)2 |
| 128t2 | 1 | 8t(4t2−4) | |||
∫ | dt = | + 16arctg(t)+C | |||
| (t2+1)3 | 2 | (1+t2)2 |
| 1 | √16−x2 | |||
∫√16−x2 = | x√16−x2+16arctg( | )+C | ||
| 2 | 4−x |
| 4 | ||
x = | ||
| 1+t2 |
| 0*(1+t2)−2t*4 | ||
dx = | dt | |
| (1+t2)2 |
| −8t | ||
dx = | dt | |
| (1+t2)2 |
| 4t | ||
xt = | dt | |
| 1+t2 |
| −32t2 | −32t2−32t4 | 32t4 | ||||
∫ | dt = ∫ | dt+∫ | dt | |||
| (1+t2)3 | (1+t2)3 | (1+t2)3 |
| −32t2 | t2 | 32t4 | ||||
∫ | dt = −32∫ | dt+∫ | dt | |||
| (1+t2)3 | (1+t2)2 | (1+t2)3 |
| −32t2 | t2 | (−8t3)(−4t) | ||||
∫ | dt = −32∫ | dt+∫ | dt | |||
| (1+t2)3 | (1+t2)2 | (1+t2)3 |
| −32t2 | t2 | −8t3 | −24t2 | |||||
∫ | dt = −32∫ | dt+ | −∫ | dt | ||||
| (1+t2)3 | (1+t2)2 | (1+t2)2 | (1+t2)2 |
| −32t2 | −8t3 | −8t2 | ||||
∫ | dt = | +∫ | dt | |||
| (1+t2)3 | (1+t2)2 | (1+t2)2 |
| −32t2 | −8t3 | (4t)(−2t) | ||||
∫ | dt = | + | dt | |||
| (1+t2)3 | (1+t2)2 | (1+t2)2 |
| −32t2 | −8t3 | 4t | 4 | |||||
∫ | dt = | + | − ∫ | dt | ||||
| (1+t2)3 | (1+t2)2 | 1+t2 | 1+t2 |
| −32t2 | −8t3 | 4t | ||||
∫ | dt = | + | −4arctg(t)+C | |||
| (1+t2)3 | (1+t2)2 | 1+t2 |
| −32t2 | −8t3+4t(1+t2) | |||
∫ | dt = | −4arctg(t)+C | ||
| (1+t2)3 | (1+t2)2 |
| −32t2 | −4t3+4t | |||
∫ | dt = | −4arctg(t)+C | ||
| (1+t2)3 | (1+t2)2 |
| −32t2 | −1−t2 | 2 | 4t | |||||
∫ | dt = ( | + | ) | −4arctg(t)+C | ||||
| (1+t2)3 | 1+t2 | t2+1 | t2+1 |
| −32t2 | 1 | 4 | 4t | |||||
∫ | dt = | (−2+ | ) | −4arctg(t)+C | ||||
| (1+t2)3 | 2 | t2+1 | t2+1 |
| 1 | √4x−x2 | |||
∫√4x−x2dx = | (x−2)√4x−x2−4arctg( | )+C | ||
| 2 | x |
| x+y | ||
arctg(x)+arctg(y) = arctg( | ) | |
| 1−xy |